On le répète à longueur d’actualité : dans le monde des intelligences artificielles, il y a évidemment les algorithmes, mais également et surtout les données d’entrainement qui sont au moins aussi importantes. Elles doivent être nombreuses et correctement étiquetées, c’est-à-dire avoir des informations fiables sur ce qu’elles contiennent.

• On développe et entraine une IA, avec seulement 10 lignes de code !

On reprend la base de données du MNIST (Modified National Institute of Standards and Technology) pour illustrer notre propos. Elle contient pour rappel 60 000 images en niveau de gris des chiffres de 0 à 9 et permet ainsi d’entrainer des intelligences artificielles à de la reconnaissance de chiffres. On peut ensuite tester l’inférence sur un autre jeu de 10 000 images. Elles sont également étiquetées, permettant ainsi de vérifier que l’IA fasse correctement son travail et obtenir un pourcentage de précision, aussi bien sur les données d’entrainement que sur des images qu’elle n’avait pas vue auparavant.

De 1 à 60 000 images d’entrainement, quelle différence ?

Mais que se passe-t-il si au lieu de prendre 60 000 images, on en prend moins ? Quelle sera l’influence sur la qualité des résultats ? Nous avons tenté l’expérience pour vous, et certains résultats peuvent surprendre au premier abord.

Première chose, un mot sur notre protocole. Nous reprenons Google Colab avec notre programme du mois de juin. Nous avons donc un réseau de neurones avec deux couches, de 25 et 10 neurones respectivement, soit près de 20 000 paramètres à ajuster.

Nous relançons l’entrainement de notre IA avec 60 000 images, puis 40 000, 20 000, 10 000, 5 000, 1 000, 100, 10 et enfin une seule image de test. Pour la sélection des images, on laisse le hasard décider, avec les lignes de code suivantes, en remplaçant le xx par le nombre d’images que l’on veut garder pour l’entrainement :

n_samples = xx
selection = np.random.choice(x_train.shape[0], n_samples, replace=False)
x_train = x_train[selection]
y_train = y_train[selection]

print('x_train shape: ',x_train.shape)
print('y_train shape: ',y_train.shape)

Les quatre premières lignes font la sélection aléatoire et remettent les données dans les variables x_train et y_train, tandis que les deux suivantes permettent d’afficher le nombre d’éléments dans chaque variable. On vérifie ainsi qu’on a bien le nombre souhaité.

Nous avons également ajouté l’importation de numpy au début, une bibliothèque permettant de manipuler les matrices. Nous exécutons trois fois chaque entrainement de notre IA, en sélectionnant bien « Redémarrer et tout exécuter » dans le menu déroulant afin de bien réinitialiser l'état de l'environnement d'exécution.

Notre programme complet et le récapitulatif des résultats

Voici donc dessous notre programme complet utilisé pour ce test (nous avons mis une sélection aléatoire de 40 000 images sur les 60 000) :

import tensorflow as tf
from tensorflow import keras
import numpy as np

mnist = tf.keras.datasets.mnist
(x_train, y_train),(x_test, y_test)= mnist.load_data()
x_train, x_test = x_train / 256.0, x_test / 256.0

n_samples = 40000
selection = np.random.choice(x_train.shape[0], n_samples, replace=False)
x_train = x_train[selection]
y_train = y_train[selection]

print('x_train shape: ',x_train.shape)
print('y_train shape: ',y_train.shape)

model = keras.models.Sequential()
model.add(keras.layers.Flatten(input_shape=[28,28]))
model.add(keras.layers.Dense(25, activation="relu"))
model.add(keras.layers.Dense(10, activation="softmax"))
model.summary()

model.compile(loss="sparse_categorical_crossentropy", metrics=['accuracy'])
history = model.fit(x_train, y_train, epochs=10)
model.evaluate(x_test, y_test)

Et, sans plus attendre, nos résultats (qui sont la moyenne de trois entrainements à chaque fois) :

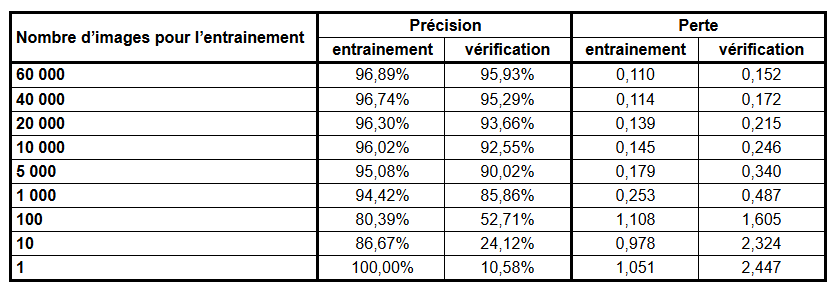
Grand écart sur la précision de 10 à 96 %

Attardons-nous sur la précision, avec un graphique représentant l’évolution du pourcentage autant sur les données d'entrainement que celles de vérification.

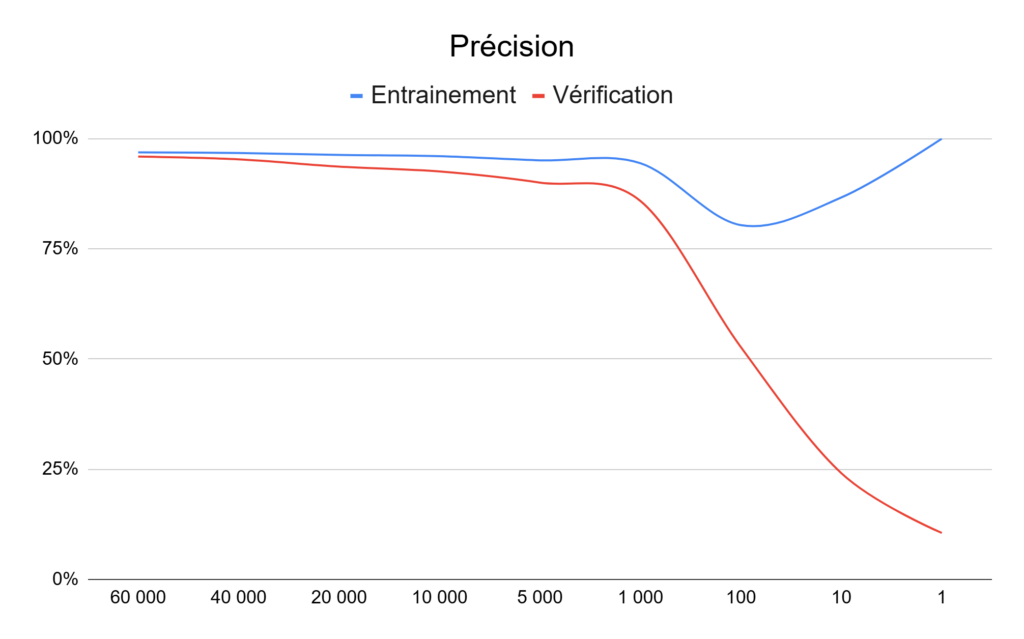
On peut voir que la courbe de la précision de l’entrainement reste au-dessus de 95 % jusqu’à 5 000 images pour l’entrainement et passe juste en dessous avec 1 000 images. La différence est assez faible entre nos trois mesures, avec moins de 0,5 point d’écart jusqu’à 5 000 images.

La chute est ensuite rapide avec 80 % avec seulement pour 100 images d’entrainement. La précision de l’entrainement « remonte » ensuite à 87 % avec 10 images et même 100 % avec une seule image. On s’en doute, ces chiffres ne veulent plus rien dire avec aussi peu de données pour entrainer notre IA.

Pour s’en convaincre, il suffit de regarder la précision lors de l’inférence sur les 10 000 images pour la vérification du modèle. On descend doucement de 96 à 90 % entre 60 000 et 5 000 images, pour ensuite passer à 86 % (1 000 images), 53 % (100 images), 24 % (10 images) et finir à 10 % avec une seule image.

Quand l’IA fait aussi bien que… le hasard

10 % de précision, cela veut dire que notre intelligence artificielle trouve le bon résultat une fois sur dix… ce qui correspond exactement au hasard. Si on avait un dé à dix face, on aurait une chance sur dix (et donc 10 %) de trouver la bonne réponse à chaque fois. Et, c'est précisément ce qui se passe dans le cas présent : l’IA trouve une fois sur dix le bon chiffre. Bref, elle ne sert à rien.

Ce cas extrême permet de montrer qu’il est facile de faire passer des vessies pour des lanternes si on ne donne pas toutes les informations. Dire qu’une IA à un taux de réussite de 100 % sur les données d’entrainement ne veut pas dire qu’elle sera performante. Dans notre cas, c'est même tout le contraire. Comme avec les statistiques, il faut voir au-delà de quelques chiffres qu’on nous met sous le nez.

C’est quoi cette perte/loss ?

Dans notre tableau, vous avez sans doute remarqué la présence d’une seconde série de mesures pour la perte, ou « loss » en anglais.

Point important avant d’aller plus loin : précision et perte ne sont pas directement liés ; ils correspondent à deux mesures de la qualité/des performances d’une intelligence artificielle.

La précision est le pourcentage de bonne réponse, tandis que la perte indique sur le niveau d’erreur de l’intelligence artificielle. Plus ses mauvaises réponses seront loin des résultats attendus, plus la perte sera importante. Pour un même niveau de précision, il est donc intéressant d’avoir le niveau de perte minimum.

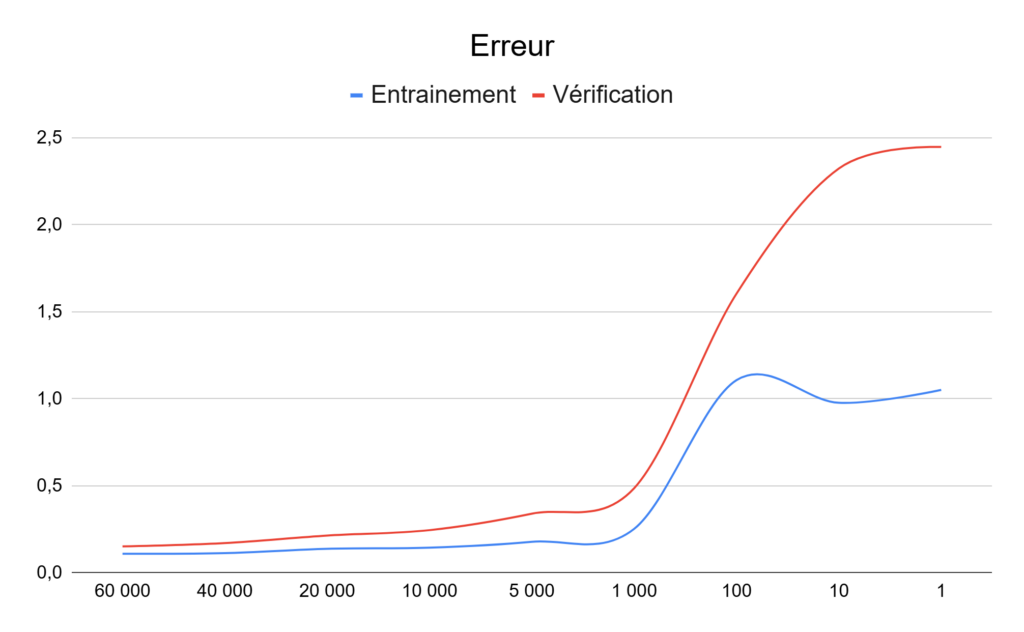
Dans un cas idéal, il faut maximiser la précision et minimiser la perte, mais les deux points ne se croisent pas toujours au même moment. Le maximum de la précision n’est pas forcément atteint lors de la perte minimale et vice-versa.

Il faut donc généralement faire des compromis : baisser un peu la précision et augmenter le niveau d’erreur, ou au contraire accepter des erreurs plus importantes et augmenter la précision. Les choix dépendront des besoins de chacun.

On peut d’ailleurs noter que notre IA arrive un peu à limiter la casse sur les données d’entrainement, mais l’erreur augmente rapidement sur les données de vérification quand le nombre d’images disponibles baisse durant l’entrainement.