Calculatrice Numworks : nombreuses améliorations avec le firmware 1.3.0, notamment sur Python

Bientôt une alternative crédible ?

Le 06 février 2018 à 14h19

6 min

Sciences et espace

Sciences

Deux mois après la précédente mise à jour, Numworks en déploie une nouvelle. Le firmware 1.3.0 apporte des changements dans quasiment toutes les applications de la calculatrice. Cette fois encore, on se demande bien pourquoi certains ont pris autant de temps.

En septembre dernier, Numworks lançait sa « calculatrice réinventée ». Problème, comme nous l'avions expliqué dans notre test en novembre, de nombreuses fonctionnalités étaient absentes lors du lancement, tandis que d'autres méritaient des améliorations. Un premier gros changement est arrivé avec le firmware 1.2.0 publié début décembre.

Il était notamment question du moteur de calcul exact pour éviter les erreurs d'arrondis. Un exemple parmi d'autres : lors de son lancement, « 1 - 0,8 - 0,2 » ne donnait pas 0 comme n'importe qui pourrait s'y attendre, mais - 5,551115e-17. L'autre gros morceau concernait l'intégration de scripts dans l'application Python.

Désormais, le firmware 1.3.0 est disponible avec, cette fois encore, des notes de versions relativement longues. Si les changements sont bienvenus, on y trouve beaucoup plus de correctifs et d'améliorations des fonctions existantes que de grosses nouveautés.

Plus de fonctions pour Python (dont input), la Toolbox s'enrichit aussi

Pour commencer, l'application Python est encore améliorée avec l'ajout d'un « module random » dans la boite à outils de la calculatrice (Toolbox). Celui-ci propose les fonctions suivantes : getrandbits, seed, randrange, randint, choice, random et uniform.

D'autres, tout aussi intéressantes, font leur apparition. Notamment input(), qui permet d'interagir avec l'utilisateur en lui demandant de saisir du texte (fonction disponible dans le menu Catalogue de la Toolbox). Enfin, min(), max() et list[m:n] (pour des tableaux) débarquent avec cette mouture 1.3.0. Là encore, des fonctionnalités assez basiques dont on se demande pourquoi elles n'arrivent que maintenant.

La Toolbox gagne trois autres fonctions : factor(n) pour décomposer un nombre en facteurs premiers, random() et randint(a,b) pour obtenir respectivement un nombre aléatoire entre 0 et 1 ou entre a et b.

Calculs de puissance de polynômes, suites liées et outils pour les fonctions

L'application Calculs peut désormais développer des puissances de polynômes – (a+b+c+...)^n par exemple –, tandis que « le symbole Ans est maintenant remplacé par son expression mathématique exacte »... un changement qui aura mis du temps à arriver. Toujours dans Calculs, la calculatrice affiche maintenant le « signe égal entre une expression et sa valeur décimale exacte dans les résultats ».

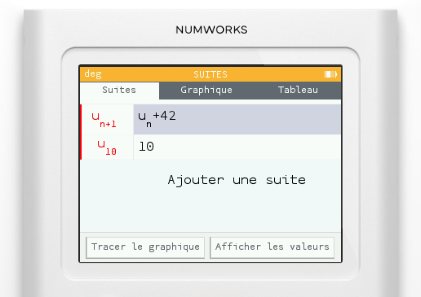
Du côté de l'application Suites, les suites liées sont utilisables, v(n) pouvant dépendre de u(n) par exemple. Par défaut, deux suites au maximum peuvent être entrées dans la calculatrice. Il faut toujours modifier le code source, le compiler et l'installer sur sa calculatrice pour augmenter cette limite.

Des outils dédiés ont été ajoutés dans les options des suites. Dans le cas d'une suite récurrente de niveau 1 ou 2, l'indice du premier terme peut être ajusté. Pour rappel, il était par défaut à 0 sur les firmwares précédents. Ainsi, au lieu de préciser u(0), vous pouvez spécifier u(10) ou u(42). On regrettera par contre que le tableau des valeurs s'obstine à commencer pour n=0 par défaut, alors que notre suite commence à u(10) par exemple.

L'application Fonctions profite également de plusieurs améliorations. Par exemple, un nouveau menu est accessible en appuyant sur OK lorsque le curseur est sur une courbe. Baptisé Calculer, il permet d'obtenir l'intersection, les maximum et minimum, les zéros, tangente et intégrale. D'autres modifications plus anecdotiques sont présentes, comme la modification du curseur (qui est désormais un point au lieu d'une croix) et l'amélioration du graphisme.

Application Probabilités améliorée, de petits correctifs par-ci par-là

Du côté des probabilités, la précision des résultats a été augmentée, les champs de texte sont étirables et s’adaptent automatiquement, les résultats peuvent être copiés et la calculatrice utilise « erf et l’inverse de erf pour la loi normale ».

Enfin, plusieurs correctifs plus généraux sont à noter : alignement des exposants, bug dans le réglage du nombre de chiffres significatifs (14 maximum depuis la mise à jour 1.2.0), soucis avec les dérivées, « amélioration des performances de la calculatrice », etc. Les notes de versions détaillées se trouvent par ici.

Les choses s'améliorent, mais il reste encore du travail pour convaincre pleinement

Si le moteur de calcul exact introduit avec le firmware 1.20 permettait à Numworks de revenir dans la course, la calculatrice souffrait encore de plusieurs manques par rapport à ses concurrentes. Cette mouture 1.3.0 en corrige certains, notamment sur les applications Suites et Python, mais ce n'est pas encore parfait... loin de là. Quelques exemples parmi d'autres : pas de conversion ou de calcul sur les unités, des interactions entre les applications trop limitées, pas de possibilité de sauvegarder ou copier des scripts Python avec son ordinateur, etc.

Néanmoins, force est de constater que deux mois après la dernière grosse mise à jour, le travail continue. Espérons que le fabricant tienne le rythme afin de proposer une calculatrice bien plus aboutie pour la prochaine rentrée des classes de lycée.

Pour rappel, la société mise sur les professeurs (elle distribue d'ailleurs gratuitement des exemplaires aux enseignants de mathématiques et mathématiques-sciences) pour pousser son produit auprès de leurs élèves... mais encore faut-il convaincre les enseignants. Si ce n'était pas franchement gagné avec le firmware 1.1.x, les choses s'améliorent grandement depuis.

Mettre à jour sa calculatrice : Chrome obligatoire

Comme toujours, il faut passer par le workshop pour effectuer la mise à jour, et obligatoirement via Chrome (à partir de la version 61). En effet, avec Edge ou Firefox, un message d'erreur indique que « le navigateur est incompatible » car « il ne dispose pas de la fonctionnalité WebUSB ». De plus, sous Windows, cette procédure nécessite l'installation d'un pilote, directement proposé par le fabricant.

La suite des étapes est classique : il faut connecter la calculatrice en USB à l'ordinateur, appuyer sur le bouton Reset sur son dos et laisser la mise à jour s'installer.

Accéder au Workshop de Numworks

Commentaires (41)

boogieplayer

Le 06/02/2018 à 15h59

KP2 a écrit :

+1

Tout le problème est dans la conversion des nombres décimaux en binaire. Les entiers passent bien mais c’est bordel pour les fractions… Et c’est loin d’etre anodin comme problème

Très très loin d’être anodin , j’ai eu un problème équivalant sur des AMD, sur certains dédié chez OVH diviser 1 par 2 ne faisait pas 0.5 mais 0.499999999999999999999999999 et du coup les tests du type if (¹⁄₂==0.5){} ne fonctionnaient pas " />

ragoutoutou a écrit :

WebUSB

Marrant, on dirait que ce mot a été uniquement créé pour tourmenter les responsables sécurité dans les grandes entreprises…

oui hiihihihihihihihi " />

Leum Abonné

Le 06/02/2018 à 16h00

ragoutoutou a écrit :

 

 WebUSB

 Marrant, on dirait que ce mot a été uniquement créé pour tourmenter les responsables sécurité dans les grandes entreprises…

Pourquoi se limiter aux grandes entreprises et aux responsables sécurité?

Je vois pas en quoi n’importe quel IT confronté a l’utilisateur moyen ne serait pas effrayé :P

jeryagor Abonné

Le 06/02/2018 à 16h00

Je trouve la tarif raisonnable : à 79,99€, c’est pas beaucoup plus cher qu’une Casio type lycée.

Uther Abonné

Le 06/02/2018 à 16h05

Exosta a écrit :

Pas vraiment, si tu lances une console Python 2.7 et que tu fais le calcul évoqué, ça te donne ce résultat. Plus de détails ici : https://docs.python.org/fr/2/tutorial/floatingpoint.html

Pas besoin d’aller chercher Python, même la console JavaScript de ton navigateur (Ctrl+Maj+K sous Firefox) te retournera le même résultat. En fait tous les langages de programmation qui suivent la norme standard des nombre flottants ont ce comportement. Ces résultats sont tout a fait normaux pour des programmeurs, parce qu’il sont censé connaitre le fonctionnement des nombre flottants (et encore j’en connais beaucoup qui ne le savent pas) qui font des arrondis sur des valeurs binaires et non décimales .

 

 Par contre il n’a aucune raison d’être attendu pour un utilisateur lambda ou même d’un mathématicien moyen qui raisonnent quasi systématiquement en décimal et non en binaire.

Donc non, ça n’était pas un bug, mais c’était quand même une absence de

fonctionnalité rédhibitoire pour une calculatrice scientifique qui montre quand même une sacré méconnaissance des attentes prioritaire des utilisateurs de ce genre de machine. Même les calculatrices 4 opérations d’il y a 40 ans, qui étaient elles aussi des machines binaires, avaient compris qu’elle devaient fonctionner en décimal.

Uther Abonné

Le 06/02/2018 à 16h10

boogieplayer a écrit :

Très très loin d’être anodin , j’ai eu un problème équivalant sur des AMD, sur certains dédié chez OVH diviser 1 par 2 ne faisait pas 0.5 mais 0.499999999999999999999999999 et du coup les tests du type if (¹⁄₂==0.5){} ne fonctionnaient pas " />

Je suppose que ça devait être plus compliqué que ça car ¹⁄₂ peut être représenté exactement en binaire. Mais de toute façon, si tu utilises des égalités strictes avec des flottants, tu mérites de toute façon la damnation éternelle " />

le podoclaste

Le 06/02/2018 à 16h19

N’exagérons rien : on peut toujours trouver la rédemption en écrivant une fonction de comparaison avec un epsilon.

Oui, comme chantait Sharon Jones : I learned the hard way…

tazvld Abonné

Le 06/02/2018 à 16h21

Papa Panda a écrit :

Décidément, elle m’intéresse vraiment.

Pour mon premier enfant quand il en aura besoin ,je pense en prendre une et voir si cela est pas que bien sur le papier.

Sauf que son prof n’en voudra pas/ qu’il n’en aura rien à cirer s’il y a un problème avec, les instructions qu’il fournira ne sera que pour les Ti voir peut-être casio.

Plouk a écrit :

Bien que ce fut corrigé, la présence d’erreurs d’arrondi à sa sortie me fait perdre toute confiance dans le produit.

Il y a de-facto un problème dans l’architecture logicielle du truc si une telle chose fut possible!

En faite, c’est directement un problème lié à la représentation des nombre décimaux en informatique. Pour faire simple, l’écriture avec des virgules n’est pas vraiment utiliser en informatique, mais on utilise une autre façon, les nombres à virgule flottante ou float, l’ordinateur écrit ça sous la forme de n*2^(f) (n et f étant des entiers) un peu de la manière d’une écriture scientifique mais uniquement avec des nombre entier

Plus exactement, c’est (-1)^sM2^(127-E) pour du float en 32 bit et (-1)^sM2^(1023-E) pour un float en 64bit ou s est le bit de signe et M et E ont une taille en bit bien défini selon que ce soit en 32 ou 64bit.

boogieplayer a écrit :

Très très loin d’être anodin , j’ai eu un problème équivalant sur des AMD, sur certains dédié chez OVH diviser 1 par 2 ne faisait pas 0.5 mais 0.499999999999999999999999999 et du coup les tests du type if (¹⁄₂==0.5){} ne fonctionnaient pas " />

oui hiihihihihihihihi " />

C’est pour ça qu’il faut privilégier pour les int des tests d’inégalité (je préfère sortir en retard que ne jamais sortir) et surtout ne jamais faire de test d’égalité avec des float.

boogieplayer

Le 06/02/2018 à 16h32

Uther a écrit :

Je suppose que ça devait être plus compliqué que ça car ¹⁄₂ peut être représenté exactement en binaire. Mais de toute façon, si tu utilises des égalités strictes avec des flottants, tu mérites de toute façon la damnation éternelle " />

tazvld a écrit :

C’est pour ça qu’il faut privilégier pour les int des tests d’inégalité (je préfère sortir en retard que ne jamais sortir) et surtout ne jamais faire de test d’égalité avec des float.

Je sais bien, mais je ne suis qu’un vermisseau face au Maître Contrôle Principal. Un être faible, fatigué par des campagnes de codes et des clients pressés.

Je dois m’absoudre " />

levhieu

Le 06/02/2018 à 16h57

Et de toute façon, ¹⁄₂ ça vaut zéro parce que 1 et 2 sont des entiers, donc le compilateur choisit d’effectuer une division entière.

KP2

Le 06/02/2018 à 17h03

ragoutoutou a écrit :

WebUSB

Marrant, on dirait que ce mot a été uniquement créé pour tourmenter les responsables sécurité dans les grandes entreprises…

" />" />" />" />" />" />" />" />" />

ComesFuxii

Le 06/02/2018 à 18h44

KP2 a écrit :

+1

Tout le problème est dans la conversion des nombres décimaux en binaire. Les entiers passent bien mais c’est bordel pour les fractions… Et c’est loin d’etre anodin comme problème

J’avais également relevé ce problème avec Excel où je devais ruser pour obtenir le bon résultat. Utilisant désormais LibreOffice Calc, je ne sais pas si le problème existe toujours sous Excel.

War Machine Abonné

Le 06/02/2018 à 19h01

boogieplayer a écrit :

Très très loin d’être anodin , j’ai eu un problème équivalant sur des AMD, sur certains dédié chez OVH diviser 1 par 2 ne faisait pas 0.5 mais 0.499999999999999999999999999 et du coup les tests du type if (¹⁄₂==0.5){} ne fonctionnaient pas " />

oui hiihihihihihihihi " />

D’un autre coté, il faut être un boulet pour faire un test d’égalité entre deux flottants. Tout enseignant d’informatique insiste sur le fait qu’il ne faut JAMAIS le faire à cause des arrondis/troncatures que font nos machines en représentation binaire, et, par conséquent, qu’il faut écrire “abs(x-y)<x*epsilon” pour tester que x est proche de y (pour x non nul).

wanou2

Le 06/02/2018 à 19h02

ComesFuxii a écrit :

J’avais également relevé ce problème avec Excel où je devais ruser pour obtenir le bon résultat. Utilisant désormais LibreOffice Calc, je ne sais pas si le problème existe toujours sous Excel.

Si je ne me trompe pas les tableurs de calculent qu’à un nombre de décimal définis qui n’est pas beaucoup plus élevés dans Cacl que dans Excel. De toutes façons un tableur n’est pas franchement fait pour faire du calcul de précision. Ce sont avant tout des outils financiers plus qu’autres choses.

Salamandar

Le 07/02/2018 à 07h49

C’est quand même la règle numéro 1 en informatique : “Tu ne feras point de comparaison d’égalité entre flottants”.

Tu parles d’AMD, mais ce problème est spécifique… Au binaire. Tout les processeurs de toutes les architectures et de tous les fabricants seront impactés. Encore pire que Spectre/Meltdown !

le podoclaste

Le 07/02/2018 à 09h00

Non, Excel utilise des flottants double précision et calcule avec les valeurs complètes, pas celles affichées (sauf pour les comparaisons, apparemment).

anonyme_69736061fe834a059975aa425bebeb6d

Le 07/02/2018 à 09h24

Pas d’accord.

Mon enfant se formera tout seul ou avec mon aide.

Comme ce fût le cas pour moi.

Sachant qu’en plus, j’ai appris à tout faire sans calculette …et servait qu’à vérifier les résultats.

Et ,perso, j’avais une ti quand les profs avait des casio.

Une calculette restera une calculette qu’elle soit de n’importe quelle marque et si un prof ,son cours dépendra d’une marque ….c’est un très mauvais prof.

ragoutoutou Abonné

Le 07/02/2018 à 09h28

Leum a écrit :

Pourquoi se limiter aux grandes entreprises et aux responsables sécurité?

Je vois pas en quoi n’importe quel IT confronté a l’utilisateur moyen ne serait pas effrayé :P

Oui mais en grande entreprise, il y a souvent un poids des dogmes sécuritaire (par opposition à une approche scientifique et raisonnée à la gestion de risques), susceptible d’engendrer une panique sévère et difficile à contenir face à un terme qui se traduit dans leur langage par ‘nitroglycérine et dynamite accrochés à une bombonne de gaz posée sur mon bureau’

Leum Abonné

Le 07/02/2018 à 09h36

Ah ça c’est clair qu’il y a un vrai problème dans la confiance qu’une maison mère pense pouvoir accorder a sa succursale qui est souvent inférieure à la confiance dont ils pourraient faire preuve par exemple.

 

boogieplayer

Le 07/02/2018 à 09h42

DayWalker a écrit :

D’un autre coté, il faut être un boulet pour faire un test d’égalité entre deux flottants. Tout enseignant d’informatique insiste sur le fait qu’il ne faut JAMAIS le faire à cause des arrondis/troncatures que font nos machines en représentation binaire, et, par conséquent, qu’il faut écrire “abs(x-y)<x*epsilon” pour tester que x est proche de y (pour x non nul).

Je sais, je ne suis qu’une pauvre merde, un développeur boulet depuis deux décennies, je ne mérite que ton enseignement " />

tazvld Abonné

Le 07/02/2018 à 10h22

Papa Panda a écrit :

Pas d’accord.

Mon enfant se formera tout seul ou avec mon aide.

Comme ce fût le cas pour moi.

Sachant qu’en plus, j’ai appris à tout faire sans calculette …et servait qu’à vérifier les résultats.

Et ,perso, j’avais une ti quand les profs avait des casio.

Une calculette restera une calculette qu’elle soit de n’importe quelle marque et si un prof ,son cours dépendra d’une marque ….c’est un très mauvais prof.

Lorsque j’étais au lycée, c’était carrément les manuels qui donnaient les instructions pour TI et Casio uniquement, sachant que le prof, même si c’était un très bon prof de math (surement l’un des meilleurs prof que j’ai jamais eu), n’avais aucune compétence dans le domaine (je pense qu’il avait en horreur les calculettes).

En soit, le cours, il peut s’appliquer à toutes les calculettes, c’est la mise en application que ça se complique. Déjà il faut arriver à faire ce que l’on souhaite faire, et les menus change complétement d’une marque à l’autre, ensuite, Casio et TI utilisent une sorte de basic, mais l’écriture n’est pas du tout la même. A ceci s’ajoute que le ³⁄₄ des lycéens sont au moins aussi ignares avec que ta grand mère dès lors que ce n’est pas leur iPhone. Ils ne connaissent pas du tout leur machine et s’en foute royalement. SI on ne leur donne pas la suite d’instruction à suivre à la lettre, ils n’y arriveront pas.

tazvld Abonné

Le 07/02/2018 à 10h28

Salamandar a écrit :

C’est quand même la règle numéro 1 en informatique : “Tu ne feras point de comparaison d’égalité entre flottants”.

Tu parles d’AMD, mais ce problème est spécifique… Au binaire. Tout les processeurs de toutes les architectures et de tous les fabricants seront impactés. Encore pire que Spectre/Meltdown !

Et la règle n°0 : tu commenceras toujours à compter à partir de 0. C’est ce qui distingue les informaticiens du reste du monde et tout particulièrement des mathématiciens (les imbéciles, ils indexent à partir de 1).

maximeK Abonné

Le 07/02/2018 à 13h29

Les mecs sont quand meme pas fut fut….  personne utilise de Float pour faire des opération mathématique en Python sinon c’est la catastrophe " />.

Ils ont changer par un Decimal et hop sa a marché, une erreur de stagiaire quand même.

La doc sur le Decimal est assez clair la dessus en plus

le podoclaste

Le 07/02/2018 à 14h44

Ne pratiquant pas Python, quel est le problème de l’utilisation des floats ? Normalement, le choix Decimal/Float est censé être plus éclairé que “personne ne l’utilise parce que c’est nul”…

levhieu

Le 07/02/2018 à 15h03

Pas sûr que tous les modules qui sont à portée de main sur un PC soient disponibles sur cette calculatrice

darth21

Le 07/02/2018 à 15h49

tazvld a écrit :

Sauf que son prof n’en voudra pas/ qu’il n’en aura rien à cirer s’il y a un problème avec, les instructions qu’il fournira ne sera que pour les Ti voir peut-être casio.

 Un prof ne peut pas refuser une calculatrice qui fait le boulot. La seule chose, c’est qu’effectivement, comme tout le monde, son prof ne connaitra probablement que ce qu’il rencontre fréquemment, soit casio et TI. Mais la numworks n’est quand même pas bien compliquée à prendre en main.

Et puis il existe quelque chose que les gens ont tendance à trop rapidement oublier, et qui peut pas mal aider à l’utilisation : le mode d’emploi. Mais encore faut-il se donner la peine de le lire …

maximeK Abonné

Le 07/02/2018 à 17h16

le podoclaste a écrit :

Ne pratiquant pas Python, quel est le problème de l’utilisation des floats ? Normalement, le choix Decimal/Float est censé être plus éclairé que “personne ne l’utilise parce que c’est nul”…

Le Float ne doit pas etre utiliser en math, car il ne se comporte pas comme un humain le pense:

ex : 0.1 + 0.1 + 0.1 - 0.3 = 5.5511151231257827e-017

Le Decimal a été implementé pour traiter ce probleme :

ex: 0.1 + 0.1 + 0.1 - 0.3 = 0

Le liens que j’ai mis l’explique clairement :)

 

levhieu a écrit :

Pas sûr que tous les modules qui sont à portée de main sur un PC soient disponibles sur cette calculatrice

Le Decimal est dans l’implementation CORE de python donc pas d’excuse ^^ 

tazvld Abonné

Le 07/02/2018 à 17h22

Celui qui le lira, ce ne sera pas le prof, et comme je l’ai dit, pour une bonne partie des lycéens, dès lors que c’est autre chose que leur iPhone, c’est au moins aussi compétent que ta grand-mère. Le mode d’emploi, c’est quelque chose qui tend à être totalement ignoré au point que même les constructeurs ne le fournissent plus.

Bien sûr qu’un enseignant ne peut pas imposer un modèle de calculatrice, mais il n’a qu’une compétence limité et ne peut pas aider les élèves qui n’ont pas la calculatrice sur lequel il a quelque compétence. Si un élève se ramène avec un modèle exotique et qu’il est incapable de faire les exercices, le prof, qui n’a pas le temps de passer des heures sur le problème, va lui faire comprendre qu’il a intérêt à se fournir avec un modèle plus classique.

le podoclaste

Le 07/02/2018 à 17h34

Ca ne rend pas le float inutilisable pour autant, même en math. Il a l’avantage de la performance et du stockage par rapport au decimal. Si tu dois placer des points dans un repère cartésien dont l’unité est le mètre et la précision le millimètre, la différence entre 5.55e-17 et 0 est négligeable.

Globalement, le decimal est meilleur pour traiter les unités monétaires, car même si tu brasses des trillions, tu ne veux pas perdre le moindre centime lors d’opérations successives. Pour les unités de grandeurs physiques, le float est applicable dans la majorité des cas.

maximeK Abonné

Le 07/02/2018 à 17h37

le podoclaste a écrit :

Ca ne rend pas le float inutilisable pour autant, même en math. Il a l’avantage de la performance et du stockage par rapport au decimal. Si tu dois placer des points dans un repère cartésien dont l’unité est le mètre et la précision le millimètre, la différence entre 5.55e-17 et 0 est négligeable.

Globalement, le decimal est meilleur pour traiter les unités monétaires, car même si tu brasses des trillions, tu ne veux pas perdre le moindre centime lors d’opérations successives. Pour les unités de grandeurs physiques, le float est applicable dans la majorité des cas.

Quand je parle en Math, c’est les maths de monsieur tout le monde  :)

SartMatt

Le 07/02/2018 à 23h05

Decimal est bien dans l’implémentation de référence de Python (CPython), mais ne fait pas partie du langage lui même, donc il n’y a aucune obligation de l’intégrer dans toutes les implémentations.

Typiquement, dans MicroPython il n’y est pas, la plupart des modules de la bibliothèque de référence ont été dégagés pour gagner de la place (MicroPython tient dans 256 Ko).

Et vues les caractéristiques matérielles de la Numworks, sont implémentation de Python est sans doute plus proche de MicroPython que de CPython.

Accessoirement, à la base le problème de précision lié au float sur la Numworks était dans son appli Calculatrice, donc ça n’a strictement rien à voir avec Python : l’application Calculatrice est écrite en C++, pas en Python.

Poppu78

Le 09/02/2018 à 09h36

Ben ouais, leçon numéro 1 sur l’usage des flottants en école d’ingé : ne jamais faire une comparaison flottante mais toujours un encadrement. On n’écrit pas if(¹⁄₂ == 0,4){} mais if(abs(¹⁄₂ - 0.5) <= 0.000000000001)) par exemple.

Tu peux renvoyer le développeur qui t’a fait ton test en formation, c’est un des trucs de base.

boogieplayer

Le 09/02/2018 à 14h10

Poppu78 a écrit :

Ben ouais, leçon numéro 1 sur l’usage des flottants en école d’ingé : ne jamais faire une comparaison flottante mais toujours un encadrement. On n’écrit pas if(¹⁄₂ == 0,4){} mais if(abs(¹⁄₂ - 0.5) <= 0.000000000001)) par exemple.

Tu peux renvoyer le développeur qui t’a fait ton test en formation, c’est un des trucs de base.

Oh oui oh oui, donne moi des leçon de dev s’il te plait " />

Tu te proposes donc que je licencie quelqu’un que tu ne connais pas, si des informations parcellaires et résumées et dans un contexte que tu ne connais pas, dans un projet que tu ne connais pas avec des contraintes techniques que tu ne connais pas. Je sais pas où tu as lu qu’il était en test et en formation, ça faudra me dire aussi.

Je te donnes le mail du DRH tu vois avec lui ?

anonyme_69736061fe834a059975aa425bebeb6d

Le 06/02/2018 à 14h26

Décidément, elle m’intéresse vraiment.

Pour mon premier enfant quand il en aura besoin ,je pense en prendre une et voir si cela est pas que bien sur le papier.

Plouk

Le 06/02/2018 à 14h33

Bien que ce fut corrigé, la présence d’erreurs d’arrondi à sa sortie me fait perdre toute confiance dans le produit.

Il y a de-facto un problème dans l’architecture logicielle du truc si une telle chose fut possible!

Exosta

Le 06/02/2018 à 14h45

Pas vraiment, si tu lances une console Python 2.7 et que tu fais le calcul évoqué, ça te donne ce résultat. Plus de détails ici : https://docs.python.org/fr/2/tutorial/floatingpoint.html

KP2

Le 06/02/2018 à 15h27

Exosta a écrit :

Pas vraiment, si tu lances une console Python 2.7 et que tu fais le calcul évoqué, ça te donne ce résultat. Plus de détails ici : https://docs.python.org/fr/2/tutorial/floatingpoint.html

+1

Tout le problème est dans la conversion des nombres décimaux en binaire. Les entiers passent bien mais c’est bordel pour les fractions… Et c’est loin d’etre anodin comme problème

levhieu

Le 06/02/2018 à 15h31

En fait, si j’étais concerné, cette succession de sorties de version pourrait bien me convaincre: c’est quand même une façon de prouver que le produit est hautement évolutif, et donc que son ouverture n’est pas inutile.

(mais je ne suis pas concerné: si j’ai besoin de faire des calculs, c’est que je suis au taf, donc en face d’un ordinateur sur lequel j’installe les packages dont j’ai besoin)

ragoutoutou Abonné

Le 06/02/2018 à 15h52

 

 WebUSB

 Marrant, on dirait que ce mot a été uniquement créé pour tourmenter les responsables sécurité dans les grandes entreprises…

le podoclaste

Le 09/02/2018 à 14h45

Ben ouais, si tu recrutais sur NXi, tu n’aurais que la crème des développeurs, ceux qui ont tout écouté en cours et rien oublié depuis.

Poppu78

Le 09/02/2018 à 14h45

Faudra donc que tu me dises où tu as lu que je proposais de le renvoyer, qu’il était en test ou qu’il était en formation. J’ai dit que tu devais le renvoyer en formation, ce qui en français signifie que tu demandes à la RH non pas de le virer mais de le former pour le mettre à niveau…

Je t’ai dit qu’il avait écrit un test (ça c’est bien toi qui nous l’as dit, ¹⁄₂==0,5 c’est bien un test dans du code…).

D’ailleurs pour être honnête, ça ne me gêne pas qu’il fasse l’erreur (je suis sûr que c’est arrivé même au plus aguerri des développeurs de la faire, c’est un classique, et c’est bien pour ça qu’on le signale dès l’apprentissage de base du code). Ce qui me gêne, c’est de s’en étonner derrière, une fois qu’on a eu le souci on le corrige, on fait son mea culpa et on passe à autre chose.

boogieplayer

Le 09/02/2018 à 16h09

le podoclaste a écrit :

Ben ouais, si tu recrutais sur NXi, tu n’aurais que la crème des développeurs, ceux qui ont tout écouté en cours et rien oublié depuis.

Le top du top des meilleurs :)

Poppu78 a écrit :

Faudra donc que tu me dises où tu as lu que je proposais de le renvoyer, qu’il était en test ou qu’il était en formation. J’ai dit que tu devais le renvoyer en formation, ce qui en français signifie que tu demandes à la RH non pas de le virer mais de le former pour le mettre à niveau…

Je t’ai dit qu’il avait écrit un test (ça c’est bien toi qui nous l’as dit, ¹⁄₂==0,5 c’est bien un test dans du code…).

D’ailleurs pour être honnête, ça ne me gêne pas qu’il fasse l’erreur (je suis sûr que c’est arrivé même au plus aguerri des développeurs de la faire, c’est un classique, et c’est bien pour ça qu’on le signale dès l’apprentissage de base du code). Ce qui me gêne, c’est de s’en étonner derrière, une fois qu’on a eu le souci on le corrige, on fait son mea culpa et on passe à autre chose.

Qu’est-ce que t’en sait de ce qu’on a fait ou pas mon petit poulet. T’as pas la moindre idée de ce qui s’est passé mais tu es gêné quand même, t’es quand même balèze. Tu te doute bien qu’on a corriger notre test sinon ça marchait pas. A moins que tu penses qu’on fait des lignes de codes qui buguent, on s’en rend compte mais laisse comme ça. J’te jure…

Mon exemple montrait que la virgule flottante fait des trucs rigolos parfois, c’est tout. Avec un ligne de code simplifiée (c’était bien plus complexe que ça en vrai) pour expliquer. Va pas t’appuyer là dessus pour faire des leçons à des gens que tu ne connait pas.

Je te donne le mail du RH tu veux gérer la formation ?