Informatique quantique, algorithme de Grover : entre mythe et espoir

La semaine dernière, nous avons attaqué la première partie de notre dossier sur l’informatique quantique. On vous a expliqué ce qu’étaient les qubits et leur principe de fonctionnement. Passons donc de la théorie à la pratique – ou presque – avec l’algorithme de Grover. Il exploite des qubits pour accélérer la recherche d’un élément dans une liste.

Avant d’entrer dans le vif du sujet, quelques rapides rappels. Dans le monde quantique, les bits sont des qubits qui valent à la fois 0 et 1. Les portes logiques manipulant les bits deviennent des portes quantiques pour qubits, avec des modes de fonctionnement différents. Elles doivent obéir aux autres règles de la physique quantique.

• Informatique quantique, qubits : avez-vous les bases ?

Les portes quantiques doivent être réversibles

Premier point important et pas des moindres : les portes quantiques doivent être réversibles. C’est-à-dire que si on réalise une opération dans un sens, il existe une autre porte capable de revenir à l’état précédent. Cela vient du fait que les opérations doivent se faire sans la moindre perte d’information.

La raison en est simple : « Les calculs quantiques doivent donc être réversibles, sinon il s’agit d’une mesure. Dans ce cas, le système perd de l’information qui est transférée à l’expérimentateur », explique Cyril Gavoille du LaBRI (Laboratoire Bordelais de Recherche en Informatique). On perd alors le caractère quantique et les avantages qui en découlent.

La bonne nouvelle, comme l’indique un autre professeur du LaBRI (Géraud Sénizergues), c’est qu’il « est cependant possible de transformer les algorithmes classiques irréversibles en algorithmes réversibles. Le prix à payer est une augmentation du volume d’information traitée et l’introduction d’une nouvelle porte logique ». Rien d’insurmontable dans tous les cas.

Résoudre un problème de recherche

Après cette petite entrée en matière, les choses vont se compliquer. On va commencer par un exemple pour bien comprendre la problématique que l’algorithme de Grover va résoudre.

Prenons un annuaire avec « N » noms classés par ordre alphabétique, chacun avec un numéro de téléphone. Si vous avez un nom, trouver le numéro de téléphone correspondant n’est pas bien compliqué. En effet, les données sont triées et de nombreux algorithmes savent parfaitement s’en sortir dans cette situation. Idem pour un humain qui trouvera rapidement l’information en feuilletant quelques pages.

Maintenant, plaçons-nous dans la situation inverse. On a un numéro de téléphone, comment l’associer à un nom ? Un être humain ne tentera surement pas l’expérience puisqu’il faudrait lire les numéros un par un, sur toutes les pages.

D’un point de vue algorithmique, il n’y a pas 36 000 solutions : on teste le premier numéro, le second… jusqu’à trouver une correspondance. Au maximum, N-1 tests sont nécessaires pour trouver la bonne solution, avec une moyenne de N/2 tests. Spoiler : l’algorithme de Grover permet de trouver le résultat – avec une très forte probabilité – pour environ √N opérations seulement.

Bien sûr, plus N est grand, plus l’algorithme de Grover est efficace. Dans un annuaire comportant 100 000 entrées, il faut en moyenne 50 000 opérations avec un algorithme classique (et jusqu’à 99 9999 si on n’est pas chanceux sur un tirage), contre 316 avec l’algorithme de Grover. Ce dernier est donc près de 160 fois plus rapide.

Avec 1 000 000 000 entrées dans l’annuaire, on passe respectivement à 500 000 000 et 31 622 tests. Grover est cette fois-ci près de 16 000 fois plus rapide que l’algorithme basique. On vous laisse faire les calculs s’il y a encore plus d’entrées dans l’annuaire.

Et voilà donc l’algorithme de Grover

Bon, assez rigolé. Accrochez-vous, ça va swinguer… et désolé par avance pour les puristes. On va en effet emprunter de nombreux raccourcis et approximations pour (tenter d’) expliquer, aussi simplement que possible, le fonctionnement de l’algorithme de Grover.

Petite précision historique : il a été inventé en 1996 par Lov Kumar Grover. C’est un algorithme très général puisqu’il ne dépend pas de la structure des données. On le retrouve comme ingrédient de base dans d’autres algorithmes quantiques.

On reste toujours dans notre annuaire N. On définit une fonction f(x) qui ne donne que deux résultats – 0 ou 1 – en fonction de x, avec x qui varie de 0 à N-1 (il y a N possibilités). La fonction se comporte ainsi : pour tous les x, f(x) = 0, sauf pour un élément x₀ qui est le bon emplacement dans notre annuaire (on ne le connait pas, mais on sait qu’il existe). Cette fois-ci, f(x₀) = 1. On reviendra plus en détail sur cette fonction f(x).

On prépare maintenant nos qubits. Par exemple, pour N = 8, cela nécessite trois qubits. Car oui, trois qubits donnent une superposition de huit états – 2³ ou 2 x 2 x 2 = 8. Si vous n’aviez pas le bon résultat, un retour rapide au premier article s’impose. Les huit états sont les suivants : |000⟩ + |001⟩ + |010⟩ + |011⟩ + |100⟩ + |101⟩ + |110⟩ + |111⟩.

Chaque état à une probabilité de 1/8. Si on « mesurait » notre qubit, on obtiendrait un des états de manière aléatoire. Un peu comme avec un dé avec huit faces parfaitement équilibrées. Avec N éléments, la probabilité est donc de 1/N.

Subtilité et charme du quantique, on utilise des amplitudes de probabilité (et pas des probabilités directement). Le prochain paragraphe n’est pas obligatoire pour comprendre le reste de l’actualité, mais il donne une explication importante.

Oracle, ô rage, ô désespoir

Dans notre précédent article, on expliquait que le qubit était présenté sous la forme |0⟩ + |1⟩ et que l’on pouvait ajouter des coefficients. On en a maintenant besoin. Notre qubit – noté |Ψ⟩ – devient alors α|0⟩ + β|1⟩, avec α² + β² = 1. α et β sont les amplitudes de probabilité (ce sont des nombres complexes). α² et β² sont les probabilités (enfin plus exactement |α|² et |β|²). Les performances de l’algorithme de Grover sont justement liées à la manière dont l’information est stockée et à l’utilisation des amplitudes.

L’algorithme de Grover entre en piste, en deux temps. Première étape, une « boîte noire » ou « oracle » détermine si l'un des états de nos qubits correspond à notre recherche, en s’appuyant sur la fonction f(x) (qui est réversible, ouf !).

Si oui, alors l’amplitude de probabilité de cet état va changer de signe pour devenir négatif. Tous les autres restent positifs. Précision importante : changer le signe ne change pas la probabilité en elle-même, puisque c’est le carré de l’amplitude.

On amplifie l’amplitude, et on recommence la boucle…

Deuxième étape : l’amplification d’amplitude. Pour cela, on calcule la moyenne des amplitudes de probabilité de tous les états. Au début, ils avaient tous la même valeur, mais puisque l’un d’entre eux est maintenant négatif, la moyenne baisse.

L’algorithme effectue ensuite une symétrie des amplitudes de chaque état par rapport à la moyenne des amplitudes (image 3 ci-dessous). Sauf pour l’état recherché, l’amplitude des autres états est très proche de la moyenne, la symétrie axiale fait donc descendre un peu la valeur.

Par contre, pour l’état dont l’amplitude était négative, la symétrie la fait remonter bien plus haut que les autres. Résultat des courses : le résultat que l’on cherche se démarque et a donc statistiquement plus de chances d’apparaitre que les autres états lors d’une mesure.

Wikipédia propose un graphique résumant bien les étapes. Les écarts sont importants dans les graphiques, ils le sont bien moins dans la pratique, surtout lorsque N augmente. Cette présentation visuelle permet néanmoins de voir le fonctionnement de Grover.

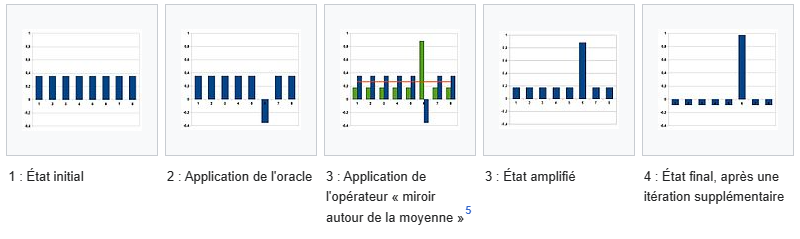
Plus N (et donc le nombre d’états) est grand, plus la différence entre l’amplitude des qubits et leur moyenne est faible. Il faut donc utiliser plusieurs fois l’algorithme de Grover pour que l’amplitude recherché augmente de manière significative (et que les autres baissent). On vous épargne les calculs mathématiques, mais il faut répéter l’opération (Pi/4)√N, souvent simplifié pour l’ordre de grandeur √N.

On a notre résultat… enfin une probabilité d’avoir le bon

Wikipédia rappelle une anecdote sur ces itérations : « C.P. Williams, dans son livre Explorations in Quantum Computing, aime citer l'épouse d'un informaticien quantique qui compare l'algorithme de Grover à la cuisson d'un soufflé : il est nécessaire d'arrêter l'algorithme ni trop tôt ni trop tard ». Trop tôt la probabilité n’est pas assez élevée, trop tard le système a continué à fonctionner pour rien.

Une fois les différentes étapes terminées, on peut mesurer le qubit. Il y a de fortes chances qu’il s’effondre (il perd sa cohérence quantique) sur le bon résultat, mais ce n’est pas une certitude à 100 %. Ce n’est pas vraiment un problème. Si le bon nombre de boucle ont été effectuées, la probabilité est suffisamment forte. Il suffit ensuite de tester le résultat pour vérifier si c’est le bon. Sinon, on relance le calcul.

Il y a une exception, si N = 4, la probabilité est alors de 100 %. Mais autant dire que c’est totalement inutile de monter un système quantique pour une recherche dans quatre éléments…

Des vidéos et une conclusion

Plusieurs vidéos sont évidemment disponibles sur Internet pour des présentations graphiques de l’algorithme de Grover. Vous pouvez par exemple regarder celle de la chaine Quantum ou de Tech Au Carré de Microsoft experiences business (plus technique). Dans cette seconde vidéo, Vivien Londe résume bien la situation :

« Le meilleur algorithme classique connu, celui qui consiste à regarder [les solutions une par une], nous fait progresser d’environ 1/N à chaque itération […] En revanche, l’algorithme quantique de Grover, à chaque étape, nous fait progresser de 1/√N. Ça vient simplement du fait que l’information quantique est stockée sous la forme d’amplitude de probabilité et non pas de probabilité. Il faut élever une amplitude de probabilité au carré pour obtenir une probabilité.
Avec du recul, l’algorithme de Grover n’exploite aucune structure dans le problème lui-même (on lui donne un problème qui n’a aucune structure), il exploite simplement la façon dont l’information est stockée dans la mémoire quantique. C’est finalement ça qui fait que l’algorithme de Grover va se retrouver en sous routine d’autres algorithmes quantiques ».

« Entourloupe » autour de l’oracle

Au fait, c’est quoi cet « oracle » ? Comment on met en place cette fonction f(x) et d’où vient-elle ? Désolé, mais nous n’avons pas la réponse pour le moment.

Vivien Londe, l’ingénieur logiciel sur la quantique chez Microsoft cité précédemment, revient un peu cette terminologie sur son GitHub personnel cette fois-ci : « Comme on ne sait pas comment cette fonction f a été inventée (ni par qui d’ailleurs), on lui donne parfois le nom d’oracle : c’est pour nous une boite noire qui nous fournit un output (0 ou 1) à chaque fois qu’on lui donne un input) ».

Sur son site personnel, Jean-François Mainguet (chercheur au CEA Leti – Laboratoire d'électronique des technologies de l'information) est bien plus remonté et n’y va pas par quatre chemins : pour lui, « il y a une entourloupe ».

« Cet algorithme est une ruse extraordinaire pour extraire un résultat particulier d'une fonction qui répond f(x)=1 pour le bon x à trouver, et f(x)=0 pour les mauvais résultats, et il faut fournir (=programmer) la fonction (l'oracle) dans l'ordinateur quantique. Et oui, on suppose que la fonction est donnée, et donc quelque part, on connait déjà le résultat, puisqu'il a fallu la programmer et donc parcourir la base de donnée ».

L'algorithme de Grover serait « bien trop surestimé »

Ainsi, pour « connecter » l’algorithme de Grover à une vraie base de données, « il faut donc entrer, par un moyen ou par un autre, une base de données qui sera une séquence de numéros {le premier numéro, le second numéro … le dernier numéro} dans une mémoire (quantique) quelconque (et là, le bât blesse) une bonne fois pour toutes […] car sinon, durant l'introduction des numéros, comme on les aura tous vus un par un, autant faire l'unique comparaison à ce moment-là, classiquement ». Pas faux.

Pour le chercheur, « on n'est pas près de voir une recherche dans un annuaire quantique fonctionner en l'état actuel des recherches. La recherche dans une base de données a encore de beaux jours dans le monde classique. Cette histoire d'algorithme de Grover est bien trop surestimée ».

Microsoft explique enfin que « l’algorithme de Grover est l’un des algorithmes les plus connus en calcul quantique. Le problème qu’il résout est souvent appelé "recherche dans une base de données", mais il est plus exact de le considérer comme un problème de recherche », justement pour les raisons que nous venons de citer.

On se donne rendez-vous au prochain épisode pour parler de l’algorithme de Shor pour factoriser un entier. C’est lui qui met à mal le chiffrement asymétrique type RSA… Du moins lorsque des machines quantiques avec suffisamment de portes et de qubits seront disponibles.