Informatique quantique, qubits : avez-vous les bases ?

L’informatique quantique, on en parle depuis des années sur Next. Les enjeux sont importants, puisque c’est une révolution sur la puissance de calcul que pourront délivrer les supercalculateurs quantiques, avec des débouchés dans plusieurs domaines (recherche, cryptographie, sciences…). On n’emploie pas de conditionnel volontairement. La question n’est en effet pas de savoir si la suprématie quantique va arriver, mais quand elle sera là.

À la base de l’informatique, il y a les bits et le langage binaire, composé de 0 et de 1 seulement. Encore maintenant, tous les ordinateurs et le monde numérique utilisent des successions de 0 et de 1. Dans les microprocesseurs et dans les ordinateurs en général, on utilise le courant électrique : tension haute pour 1, tension basse pour 0. Il existe bien d’autres mécanismes, notamment l’orientation d’un champ magnétique pour stocker des données sur les disques durs.

Des portes pour manipuler des bits

Puisque les données en informatique se résument à des bits, effectuer des opérations revient à les manipuler. On utilise pour cela des portes logiques. Elles prennent des bits en entrée, réalisent des opérations logiques et donnent des bits en sortie. Jusqu’ici, tout va bien.

Il y a des portes NOT ou « inverseur » (0 devient 1 et vice-versa), puis de nombreuses autres portes pour comparer des bits : AND ou « et logique », OR ou « ou inclusif », XOR ou « ou exclusif », etc. Ces portes logiques, on sait parfaitement les mettre en œuvre en électronique, particulièrement avec des transistors… que l’on retrouve dans les processeurs (et ce n’est pas un hasard). Il faut parfois de nombreux transistors pour créer une seule porte.

On enchaine les portes pour les opérations mathématiques

Les opérateurs de base tels que la multiplication et l’addition ne sont pas disponibles par défaut, mais on peut les créer. On va uniquement expliquer le fonctionnement de l’addition, avec deux bits en entrée : « A » et « B », qui peuvent chacun valoir 0 ou 1.

Trois résultats sont possibles : 0 (si les deux sont à 0), 1 (si un est à 1 et l’autre à 0) et 2 ou 10 en binaire (si les deux valent 1). Pour l’addition, on utilise pour cela deux portes logiques : XOR et AND. La page Wikipédia donne de bonnes explications sur ce principe.

C’était la version simple. On ne détaillera pas ici la multiplication de bits, mais sachez que cette opération est bien plus complexe et nécessite aussi d’utiliser l’addition. Éric Peronnin, de l’université de Nantes, propose une explication en vidéo (et de nombreuses autres vidéos sur sa chaine). Si le sujet vous intéresse, nous pourrons y revenir dans un second temps.

On résume : un ordinateur (et n’importe quelle machine informatique classique) ne fait que manipuler des bits. Ces derniers passent dans des portes logiques pour réaliser des opérations mathématiques en fonction des besoins des algorithmes. Chaque opération peut nécessiter plusieurs portes et chaque porte plusieurs transistors. Ce n’est d’ailleurs pas sans conséquences sur la gestion des nombres en informatique.

• Les nombres en informatique : entiers, virgule flottante, simple et double précision (FP32/64), Tensor Float (TF32)…

Et voilà les qubits, qui valent à la fois 0 et 1

Passons maintenant à l’informatique quantique. Pour faire simple, on change à partir de la base. On laisse de côté les bits pour les qubits (ou q-bits), c’est-à-dire des bits quantiques. Hé oui… on va parler un peu de physique quantique, qui est à la base de l’informatique quantique.

Il nous faut pour cela introduire plusieurs notions, à commencer par le principe de superposition. Si les bits ne peuvent prendre que deux valeurs exclusives (c’est bien l’une OU l’autre), les qubits peuvent exister dans une superposition des états 0 et 1. On peut aussi dire qu’ils sont dans les deux états à la fois, ils valent à la fois 0 et 1. En physique, on utilise la notation |0⟩ + |1⟩ pour représenter cette superposition. On peut ajouter des coefficients devant chaque état, mais restons simples (du moins autant que possible).

Lorsqu’on effectue un calcul avec un qubit, on obtient donc le résultat final pour 0 et pour 1, alors qu’il aurait fallu deux calculs avec un bit classique. Mieux encore, le gain de performances est exponentiel lorsque le nombre de qubits augmente.

Deux piliers des qubits : superposition et intrication

Avec 3 qubits, on a une superposition des huit états suivants : |000⟩ + |001⟩ + |010⟩ + |011⟩ + |100⟩ + |101⟩ + |110⟩ + |111⟩. Une opération sur ces qubits la réalise donc sur chaque état en une seule fois, alors qu’il faudrait huit opérations (une pour chaque possibilité) sur un ordinateur classique.

Avec trois bits, on code les entiers de 0 à 7 (huit au total), tandis qu’avec trois qubits, on code les entiers de 0 à 7 et toutes leurs superpositions. Si on calcule une fonction f(x) avec x un qubit, alors on obtient le résultat des huit états en une seule fois. Avec quatre qubits, on passe à 16 états, avec cinq qubits à 32, etc. De manière générale, un ordinateur quantique avec n qubits ira 2^n fois plus vite qu’un ordinateur classique.

On parle ici de plusieurs qubits, comme si c’était aussi simple que les « poser » les uns à côté des autres. C’est bien plus compliqué. Il faut en effet que les qubits soient intriqués (ou enchevêtrés). L’intrication quantique « est un phénomène dans lequel deux particules (ou groupes de particules) forment un système unique, et présentent des états quantiques dépendant l'un de l'autre quelle que soit la distance qui les sépare », explique le CEA. IRIF, une unité mixte de recherche entre le CNRS et l'Université Paris Cité, donne une précision importante : « Sans intrication, aucun avantage quantique n'est possible ». Et plus il y a de qubits, plus l’intrication est complexe.

« Grâce à ces deux phénomènes, la superposition et l’intrication, un ordinateur quantique peut en théorie avoir accès à la totalité des résultats possibles d’un calcul en une seule étape, là où un ordinateur classique doit traiter l’information de façon séquentielle, un résultat après l’autre. C’est ce parallélisme massif qui est au cœur de la puissance de l’ordinateur quantique », ajoute le CNRS.

Pour une explication en images, IRIF, propose QuBobs. Il s’agit d’un « projet de vulgarisation scientifique qui a pour but de fabriquer des objets interactifs, pédagogiques et ludiques pour expliquer les principes de base de l'ordinateur quantique ». Dans le cas des qubits, ils sont représentés par des disques colorés.

Les portes logiques deviennent quantiques

Comme en informatique classique, il faut maintenant faire passer ces qubits dans des portes logiques pour réaliser des opérations. Il faut par contre des portes quantiques, qui sont bien différentes des portes classiques.

Commençons avec la porte de Hadamard. Elle prend un qubit en entrée et permet de transformer un état non superposé de |0⟩ ou |1⟩ dans un état superposé de |0⟩ et |1⟩. On a aussi la porte de Pauli-X, qui est l’équivalent quantique de la porte NOT. Elle transforme donc un |0⟩ en |1⟩ et vice-versa. Vous trouverez d’autres portes quantiques sur Wikipédia ou dans cette « introduction » du Collège de France, mais il faudra vous accrocher pour bien les comprendre.

Avec 300 qubits, on cartographie le Big Bang

Inria s’aventure à une estimation des possibilités lorsque l’on disposera de centaines de qubits dans un calculateur quantique : « On estime ainsi que près de 300 qubits parfaitement enchevêtrés en superposition pourraient cartographier toutes les informations de l'univers à partir du Big Bang »

À VivaTech en juin dernier, France Hybrid HPC Quantum Initiative présentait aussi quelques chiffres. Avec 50 qubits intriqués, on a « plus d’états que n’importe quel supercalculateur ». Avec 300 qubits (toujours intriqués évidemment), on dépasse le nombre d’atomes dans l’Univers, excusez du peu.

Petite digression sur ces gros chiffres. Le nombre d’atomes dans l’Univers (observable) est d’environ 10⁸⁰ (on n’est pas à quelques zéros près à ce stade). 300 qubits donnent 2³⁰⁰ états, un chiffre de l’ordre de 10⁹⁰. Selon le mathématicien Claude Shannon, il y aurait environ 10¹²⁰ parties « intéressantes » à jouer aux échecs, et on monte à 10⁷⁶⁸ combinaisons au jeu de Go. Vous pouvez aussi vous perdre sur cette page Wikipédia.

• • Des échecs au jeu de Go : quand l’intelligence artificielle dépasse l’homme

La décohérence est l’ennemie des qubits

Là encore, c’est la théorie. En pratique, c'est une nouvelle fois bien plus compliqué. Avec quelques dizaines de qubits, on fait beaucoup de choses sur le papier, alors qu’on ne fait vraiment pas grand-chose dans la pratique.

Comme avec les bits, il faut passer un très grand nombre de portes pour terminer un algorithme. Problème avec les qubits : il faut les garder dans un état quantique, avec superposition et intrication, pendant tout le processus. Sous l’effet de son environnement (et d’autres paramètres), la superposition quantique se dégrade plus ou moins vite, aboutissant inexorablement à une décohérence des qubits.

Les facteurs sont nombreux : « modifications des champs magnétiques et électriques, rayonnement d'objets chauds à proximité ou interactions non contrôlées entre les qubits », explique Inria. « La décohérence affecte l'état de superposition et perturbe le traitement quantique de l'information. Cela conduit à des erreurs dans les systèmes de calcul quantique. Alors qu’un ordinateur classique se révèle très fiable, un ordinateur quantique ferait une erreur sur 1 000 opérations (pour les meilleurs d’entre eux) », ajoute l’Institut.

On peut faire une analogie avec une pièce de monnaie lancée en l’air, quand elle tourne sur pile et face à la fois. Lorsqu’elle tombe sur une surface, elle vient se figer dans une des deux positions, c’est l’équivalent de la décohérence.

On en revient aussi à l’exercice de pensée du chat de Schrödinger qui est à la fois mort et vivant tant qu’on n'a pas regardé dans quel état il se trouve. Bien évidemment, c’est totalement impossible pour un chat qui n’est pas un objet quantique, mais c’est l’idée générale.

L’indispensable correction d’erreur

Pour réduire les erreurs et améliorer la durée de vie des qubits, on passe sur des qubits logiques, qui sont un assemblement de qubits physiques. Un qubit utile pour un calcul n’est donc plus un qubit, mais des dizaines, centaines ou milliers de qubits.
Pour Intel, la correction d’erreur « est considérée comme le seul moyen de produire un ordinateur quantique à grande échelle avec des taux d'erreur suffisamment faibles pour des calculs utiles. Au lieu de calculer sur les qubits individuels eux-mêmes, nous calculerons ensuite sur des qubits logiques. En codant un nombre plus important de qubits physiques sur notre processeur quantique en un seul qubit logique, nous espérons réduire les taux d'erreur pour activer des algorithmes quantiques utiles ».
Le CNRS ajoute un point motivant pour les chercheurs : « il a même été démontré que, en théorie, si le taux d’erreur d’un qubit est inférieur à une certaine valeur, alors il est possible de corriger les erreurs plus vite qu’elles ne se forment ». C’est « une petite révolution dans le domaine, ajoute Sébastien Tanzilli (Institut de physique de Nice et représentant de la France au Quantum Community Network). Avec elle, même les plus pessimistes ont commencé à croire en la possibilité d’un ordinateur quantique ».

Assembler des qubits physiques pour en faire des logiques

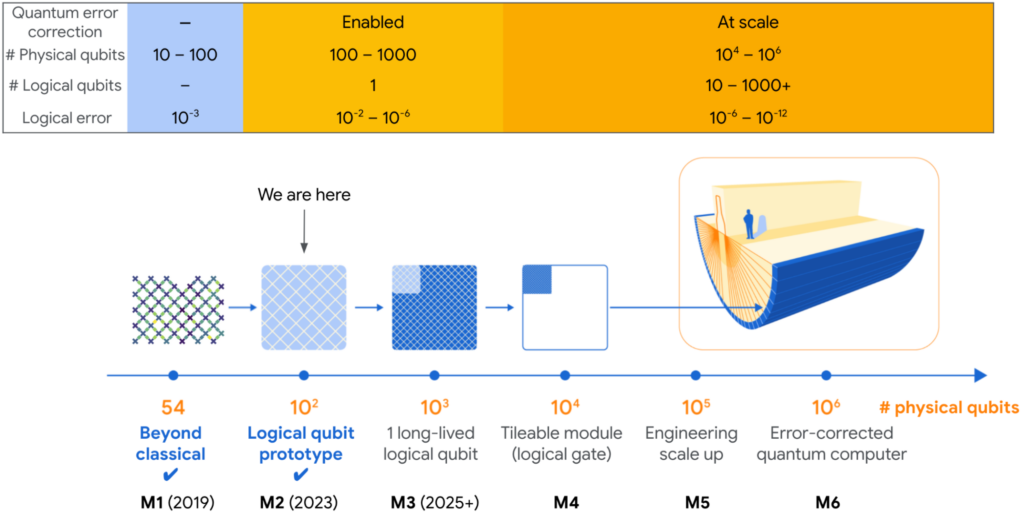
Au début de l’année, l’entreprise présentait son travail sur la correction d’erreur, avec une perspective sur les prochaines années. De quelques dizaines de qubits physiques pour un seul qubit logique en 2023 avec un taux d’erreur de 1 pour 100, Intel compte passer à 1 000 qubits physiques pour un seul qubit logique, mais avec une durée de vie plus longue et surtout un taux d’erreur de 1 pour 100 000.

Au CNRS, « on estime qu’il faudrait 1 000 – voire 10 000 – qubits physiques pour chaque qubit logique utilisable pour les calculs. Autrement dit, l’ordinateur quantique idéal devrait comporter non pas quelques milliers de qubits, mais quelques millions ! ».

Et maintenant, le résultat final

Vous pensez que c’est la fin ? Pas si vite… il faut encore extraire le résultat sous une forme exploitable. Dans le vocabulaire de l’informatique quantique, le ministère de la Recherche et de l’Enseignement brosse une présentation générale :

« Un algorithme quantique manipule une grande quantité d'informations pendant le calcul mais produit un résultat sous la forme de bits classiques. Le calcul doit être généralement répété plusieurs fois pour obtenir le résultat recherché. Un algorithme quantique est écrit et exécuté à l'aide d'un ordinateur classique qui envoie des commandes de portes quantiques au processeur quantique puis, à la fin du calcul, récupère et exploite les résultats issus de la lecture des qubits ».

Hé oui, on n’est pas toujours certain d’avoir le bon résultat à la fin. Mais comme le calcul est rapide, ce n’est pas forcément un souci de le lancer plusieurs fois. Nous y reviendrons dans un prochain épisode sur les algorithmes de Grover et de Shor, entre autres. Par la suite, on parlera des qubits en eux-mêmes pour se rendre compte qu’il n’y a pas une informatique quantique, mais des informatiques quantiques.