Dans le cadre de notre dossier sur l’informatique quantique, nous avons déjà expliqué ce qu’étaient les qubits, des bits qui valent à la fois 0 et 1 (pour simplifier). On ne parle plus de portes logiques, mais de portes quantiques avec des modes de fonctionnement différents. Elles doivent notamment obéir aux autres règles de la physique quantique, et donc être réversibles. Rien d’insurmontable, mais cela implique bien souvent une augmentation de la complexité du traitement des données. Le gain se fait sur la vitesse de calcul, qui est sans commune mesure.

Nous avons également détaillé le principe de fonctionnement de l’algorithme de Grover, un exemple pratique de l’utilisation de l’informatique quantique… modulo tout de même l’utilisation de l’« oracle » aussi appelé « boîte noire ». Passons maintenant à un autre algorithme qui fait couler beaucoup d’encre au cours des dernières années : celui de Shor.

• Informatique quantique, qubits : avez-vous les bases ?
• Informatique quantique, algorithme de Grover : entre mythe et espoir

En 1994, Peter Shor chamboule la cryptographie

Conçu par Peter Shor en 1994 (il y a donc tout juste 30 ans), l’algorithme éponyme permet entre autres de casser le chiffrement RSA en un temps polynomial au lieu d’exponentiel. Cela ne vous parle pas ? Disons les choses autrement : alors qu’un ordinateur classique aurait besoin de plusieurs milliards d’années pour factoriser un grand nombre (permettant de casser RSA qui se base sur la factorisation), cela ne prendrait que quelques minutes à une machine quantique.

Il y a quelque temps, Vivien Londe (spécialiste quantique chez Microsoft, ex-doctorant Inria) expliquait dans la Tech au carré que pour factoriser un nombre de 1024 bits, il fallait plusieurs millions d’années sur un ordinateur classique. Avec 2048 bits, on passerait à seulement quelques minutes sur un ordinateur quantique, à condition qu’il dispose de suffisamment de qubits et de portes, ce qui est un des plus gros facteurs limitants actuellement. Et ce n’est pas à prendre à la légère !

Dans un document publié par Loria (Laboratoire lorrain de Recherche en Informatique et ses Applications, une unité mixte de recherche), on explique que la « la factorisation d’un entier de n bits nécessite un ordinateur quantique parfait avec 2n qubits (bits quantiques) ».

Pour d’autres, il faut (3n+0,002 x n x log(n)) qubits. Avec la correction d’erreur, on multiplie le nombre de qubits par 10, 100, 1000 voire plus. Vous avez dans tous les cas un ordre d’idée du nombre de qubits. Pour faire simple, beaucoup : des (dizaines/centaines de) milliers. Les qubits physiques sont regroupés par paquets de 10, 100, 1000 ou plus pour former un seul qubit logique, utilisable dans les calculs.

Shor n’est pas un « casseur » universel de cryptographie

Précision importante : l’algorithme de Shor et l’informatique quantique ne sont pas capables de casser tous les systèmes de chiffrements. Shor ne s’attaque qu’à la factorisation et donc pas à des algorithmes utilisant une autre méthode.

Dans le cas d’un algorithme symétrique comme AES, il suffit de doubler la taille des clés pour être paré pour les ordinateurs quantiques. Si on passe, par exemple, d’AES sur 256 bits avec un ordinateur classique à de l’AES 512 sur une machine quantique, on a à peu près le même niveau de résistance. Pour casser AES, il faudrait donc trouver une autre méthode… si elle existe.

• • Le chiffrement hybride classique et post quantique, comment ça marche

Fonctionnement de l’algorithme de Shor

Pour en revenir au fonctionnement de Shor, c’est en fait un algorithme hybride. Il a une partie classique et une autre quantique. Cette dernière concerne la recherche d’ordre d’une fonction. Il faut, pour mettre en place Shor, disposer d’un registre de n qubits, n étant le nombre de bits du nombre que l’on souhaite factoriser.

Pour une explication plus technique (et mathématique), on vous laisse regarder la vidéo de la chaine Quantum avec Arnaud Bodin de l’université de Lille. Attention, les explications (compliquées et demandant de solides connaissances en mathématiques) sont en plusieurs vidéos, la dernière partie étant la 13.4.

Vous avez également des cours en ligne (à partir de la page 155), avec un exemple pratique de l’algorithme de Shor sur la factorisation du nombre 15. Spoiler : c’est 3 x 5. Bien évidemment, le quantique et même les ordinateurs classiques ne sont pas nécessaires dans ce cas.

Des milliers de qubits… encore plus avec la correction d’erreur

Toujours selon Vivien Londe, avec « un ordinateur quantique de 6 000 qubits parfaits et capable de faire de l’ordre de 10 milliards d’opérations, on met en danger tout un pan de la cryptographie actuelle ». Mais il faut nuancer ces estimations, ajoute-t-il, car les qubits que l’on fabrique actuellement sont en nombre bien inférieur, en plus de ne pas être parfaits.

Leur « taux d’erreur est assez élevé, et donc pour arriver à mettre en place l’algorithme de Shor, il faut utiliser des techniques de correction d’erreur. On considère en première approximation qu’il faut multiplier par 1 000 le nombre de qubits utilisés ». On passe donc de 6 000 à 6 000 000 de qubits. Les machines actuelles en ont généralement quelques dizaines. Le chemin est encore long.

Shor fonctionne : 15, 21, 143, 56153…

Quoi qu’il en soit, l’algorithme de Shor fonctionne, et on le sait depuis des années. En 2001, une équipe d’IBM Research-Almaden à San José publiait dans la revue Nature la « première réalisation expérimentale publiée de l’algorithme de Shor ». L’algorithme avait été publié sept ans auparavant seulement.

Alors oui, c'était juste pour trouver que « 15 = 3 x 5 », mais « leurs travaux ont été parmi les premiers à montrer que l’informatique quantique était plus qu’une simple expérience de pensée », explique IBM. La machine quantique disposait de sept qubits.

Il y a quelques années (2018), le CNRS rappelait que, en 2012, « la plus belle prouesse calculatoire » de l’époque avait été accomplie par une équipe de l’université de Bristol, en Angleterre. Elle était « parvenue à factoriser 21, soit à montrer que ce nombre se décompose en 3 fois 7, grâce à un dispositif photonique ». Autant dire que l’on progresse lentement… 11 ans pour passer de 15 à 21. Un an plus tard, en 2013, c’était au tour de 143 (11 x 13).

Shor n’est pas le seul algorithme sur les rangs de la factorisation, comme le rappellait Olivier Ezratty dans un article de 2018. « Depuis, on est juste passé à un nombre à 5 chiffres, 56153 […] mais avec un autre algorithme de factorisation que celui de Shor. C’est en fait un algorithme d’optimisation qui fonctionnait sur ordinateur à recuit quantique du Canadien D-Wave ! Le record à ce jour atteint en 2016 serait la factorisation de 200 099 avec 897 qubits sur D-Wave ». D-Wave et le recuit quantique, c’est une autre histoire que nous détaillerons dans un prochain article.

…et même 4 088 459 ont été factorisés en quantique

« Le record de factorisation quantique actuel est ridiculement petit : il s’agit de 4 088 459 = 2017 × 2027 en 2018, et encore il est loin d’être clair que le procédé utilisé permette de factoriser n’importe quel nombre de 7 chiffres. Bref, il est fort probable que RSA-1024 sera factorisé bien avant que l’ordinateur quantique entre dans la course », expliquaient des chercheurs en 2020 dans un article intitulé « Nouveaux records de factorisation et de calcul de logarithme discret ».

« L’exploit » a été réalisé sur une machine IBM avec 5 et 16 qubits. On place des guillemets, car on peut obtenir le même résultat avec des logiciels de factorisation sur n’importe quel ordinateur ou même sur des sites web, en largement moins de temps qu’il en faut pour écrire cette phrase. Il n’en reste pas moins que Shor fonctionne, mais l’algorithme est encore loin d’avoir fait tomber RSA et les autres systèmes de cryptographie fondés sur la factorisation.

Portes logiques et temps de calcul : deux autres éléments importants

Comme expliqué au début, les qubits ne font pas tout : il faut avoir des portes en quantité suffisante, mais également que le système soit capable de rester dans son état quantique pendant toutes les opérations.

Selon un article publié en 2019 et repris par Devoteam Revolve sur son blog, il faudrait 0,3 x n³+ 0,005 x n³ x log(n) portes logiques. Avec un nombre sur 2048 bits (RSA-2048 avec 617 chiffres par exemple), il faudrait donc plus de 6 000 qubits (on retombe sur les estimations de Viven Londe), mais aussi plus de… 2,7 milliards de portes logiques. Et encore, c’est sans compter qu’il faudrait que le système quantique soit capable de tenir plusieurs heures, on en est très (très (très…)) loin.

Les chercheurs ont publié des graphiques intéressants sur leurs estimations. Sur le premier, on peut voir le temps nécessaire en fonction de la taille (en bits) du nombre à factoriser et de la méthode utilisée, sur le second le nombre de portes et de qubits nécessaires.

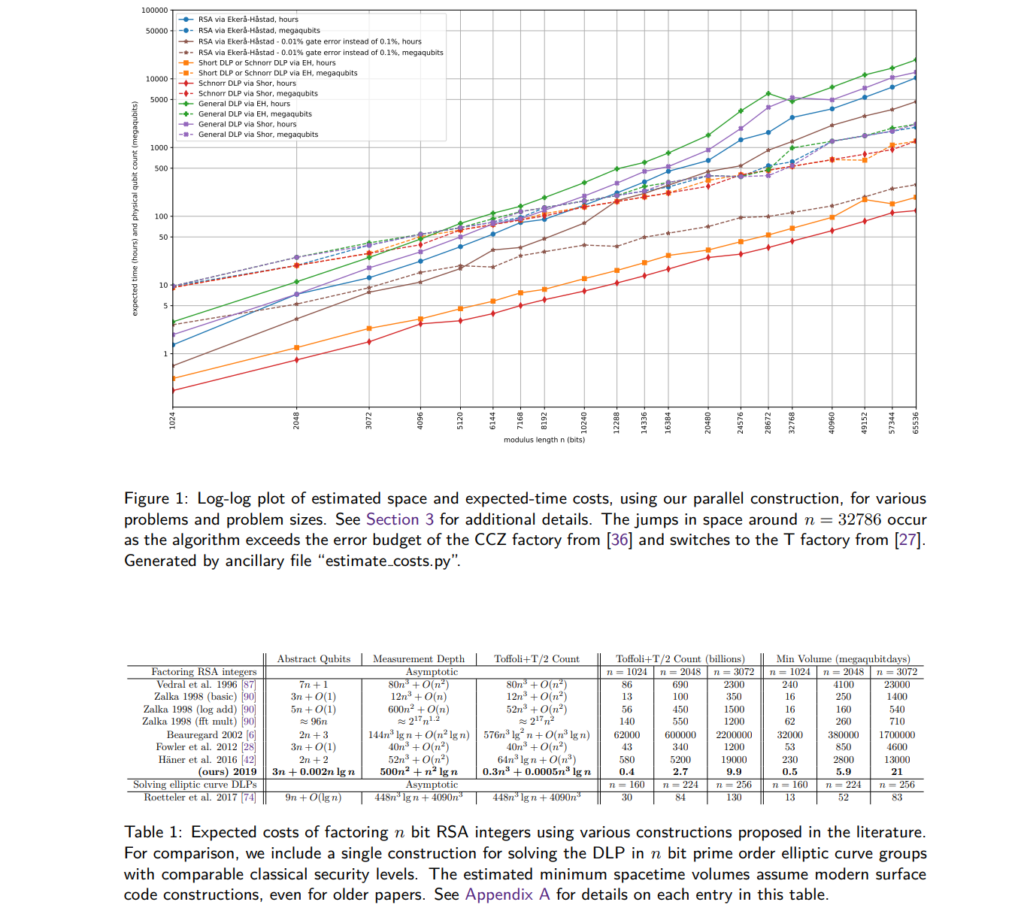
Shor motive la recherche sur l’informatique quantique

Oui, l'algorithme de Shor fonctionne, c’est prouvé. Mais il est encore loin de mettre à mal RSA dans la pratique à cause de la complexité technique requise pour sa mise en œuvre. Il n’en reste pas moins que cet algorithme a révolutionné l’informatique quantique : « La découverte de Shor est l’une des motivations principales pour construire un ordinateur quantique », expliquait le chercheur André Chailloux en 2017.

Ce dernier ajoute que, « en 1994, Peter Shor a montré qu’avec un ordinateur quantique, on pourra factoriser des nombres qui auront des milliers voire des millions de chiffres », contre quelques centaines avec un ordinateur classique (y compris les supercalculateurs).