Depuis 15 ans, les nouveaux services décentralisés se multiplient, facilitant le travail en équipe et le partage de fichiers, permettant de se passer d'une « autorité centrale ». Comme souvent dans l'informatique moderne, cela doit beaucoup à des travaux menés à la fin des années 70, dont les arbres de Merkle.

L'outil de gestion des versions Git a été créé en 2005 par Linus Torvalds. Le livre blanc décrivant Bitcoin a été publié par Satoshi Nakamoto en 2008. IPFS a été initié par Juan Benet en 2013. Outre leur volonté de décentraliser les usages et services, ces trois projets partagent un point commun : ils exploitent des arbres de hachage.

• Apprenez à utiliser Git : les bases pour suivre l'évolution d'un document

Ils sont loin d'être les seuls. Il y a bien entendu de nombreuses crypto-monnaies et systèmes de transferts pair-à-pair (P2P), mais on peut également citer les systèmes de fichiers Btrfs et ZFS, Apache Wave (ex-Google Wave), des gestionnaires de paquets, des bases NoSQL, etc. Tous les implémentent d'une manière ou d'une autre.

Selon Wikipédia, il s'agit d'une « structure de données contenant un résumé d'information d'un volume de données, généralement grand [...] le principe d'un arbre de hachage est de pouvoir vérifier l'intégrité d'un ensemble de données sans les avoir nécessairement toutes au moment de la vérification ».

Mais en pratique, comment ça fonctionne et en quoi cela change la donne ? On vous explique tout.

Au commencement était le hash

En cryptographie, un hash est le résultat d'un calcul désignant des données avec une taille fixe, de manière déterministe, unique et non réversible. C'est pour cela que l'on parle aussi d'empreinte en français. Par exemple, si vous téléchargez l'image ISO d'Ubuntu 21.04 Desktop (amd64), son empreinte SHA-256 est la suivante : 

fa95fb748b34d470a7cfa5e3c1c8fa1163e2dc340cd5a60f7ece9dc963ecdf88

Cela veut dire que si vous téléchargez le fichier et que son contenu est 100 % conforme, calculer son empreinte SHA-256 donnera le résultat ci-dessus, elle est donc déterministe. Vous pouvez ainsi en vérifier simplement l'intégrité. Mais depuis cette seule empreinte, vous ne pouvez pas retrouver le contenu du fichier (non réversible).

De plus, si des « collisions » peuvent survenir (deux fichiers avec une empreinte similaire), une fonction de hachage doit répondre à quelques critères. Ces collisions doivent être rares et ne pas pouvoir être créées ou devinées. On ne doit ainsi pas être capable de générer un faux bloc de données ayant la bonne empreinte. De plus, le changement du moindre bit dans le fichier doit significativement modifier l'empreinte pour éviter de trouver des similarités. C'est en cela que l'empreinte d'un fichier est en général considérée comme unique.

L'arbre de hachage permet d'appliquer ces règles à l'échelle de petits blocs de données avec une hierarchie simple à parcourir. Ainsi, plutôt que d'avoir une seule empreinte par fichier, on en calcule pour de nombreuses portions. Cela permet de vérifier l'intégrité de chacune d'entre elles, mais aussi d'éviter les doublons, de comparer ceux qui ont changé entre deux versions d'un fichier. Tout l'enjeu étant d'y parvenir de manière efficace.

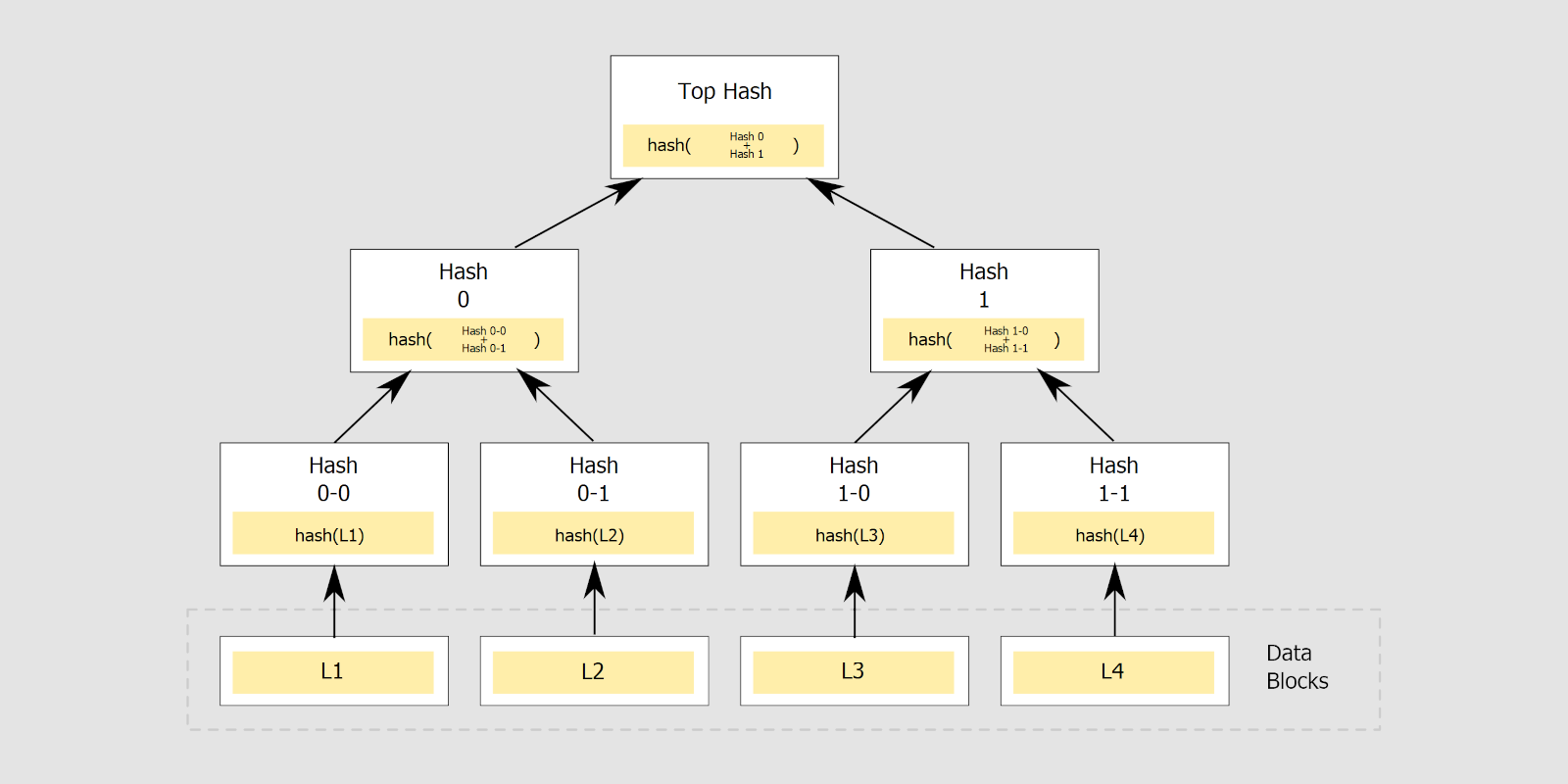
Un arbre de Merkle dit binaire : chaque élément dispose de deux nœuds maximum

Arbre des années 80...

C'est ce qu'a réussi Ralph Charles Merkle, célèbre cryptographe américain connu pour ses puzzles (pour l'échange de clé en vue d'une communication chiffrée) et la construction Merkle–Damgård utilisée dans la fonction de hachage MD5 (d'où les initiales), mais également dans de plus récentes comme SHA-1 et SHA-2.

En juin 1979, alors qu'il étudie à Stanford, il publie une thèse de 182 pages, fruit de 5 ans de travail : Secrecy, Authentication, and public Key Systems. On y découvre les « arbres d'authentification », qui font l'objet d'un dépôt de brevet (US4309569A) la même année, accordé en 1982, expiré en 1999.

En pratique, un arbre de Merkle est constitué de blocs de données considérés comme ses feuilles (leaf nodes), situés dans la partie inférieure de la représentation en graphe. Pour chacun de ces blocs, on calcule une empreinte. Ils sont ensuite organisés en branches, chacune contenant les empreintes de ses feuilles, ce qui constitue de nouvelles données, dont on calcule l'empreinte. On remonte l'arbre jusqu'à obtenir l'empreinte racine.

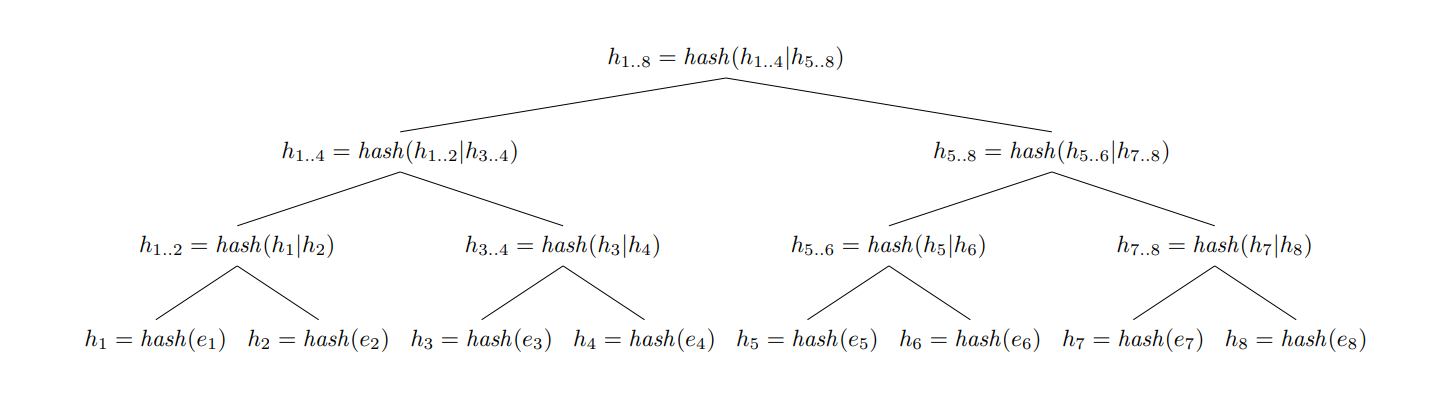
Chaque empreinte calculée est unique, comme celles de chaque branche ou de chaque feuille. On peut ainsi vérifier l'intégrité du fichier dans son ensemble ou de branches plus ou moins importantes selon le découpage opéré. Cette organisation permet d'ailleurs d'effectuer des vérifications même si l'ensemble de l'arbre n'est pas connu.

Cela permet aussi de moduler le besoin de confiance lorsque l'on récupère les données depuis une multitude de sources. On peut chercher à s'assurer de la fiabilité de l'empreinte principale par des moyens complexes en étant plus laxiste sur la composition de l'arbre et la récupération de ses données puisque l'on peut vérifier si elles sont conformes au résultat attendu et changer de source si ce n'est pas le cas, garantissant la sécurité de la procédure.

Comprendre les arbres de Merkle par l'exemple

Pour mieux illustrer l'intérêt de cette solution, prenons l'exemple d'un simple texte :

Hello, World !

Calculons son empreinte via la fonction SHA-256 (sous Linux) :

echo "Hello, World !" | sha256sum
114b850f2f0959c5f98664f3d8d9345742d713923bd24b2f049b6af66d4e31f6 -

Modifions maintenant un caractère et recalculons l'empreinte :

echo "Hello, Warld !" | sha256sum
5631e5f6bbd88e0093955bc303ba1f5a0acf6081b8d41fc47a9d6213c1716b64 -

La différence entre les deux empreintes nous permet de voir que les données sont différentes, sans pour autant savoir que 13 des 14 caractères de ce texte sont identiques, soit 93 % ! C'est là que l'arbre de Merkle entre en scène.

Découpons ce texte sous la forme d'un arbre composé de quatre feuilles contenant chacune quatre caractères, dont on calcule l'empreinte. On les regroupe par branches de deux feuilles, qui contiennent les deux empreintes l'une à la suite de l'autre. On calcule ainsi l'empreinte de la branche, puis de la racine.

Dans le cas du premier texte, cela donne le résultat suivant :

Racine -> 5108ad59f7bbcc22901e82a3940820724220566bb13339bd4987ae224333590e
 
Branche 1 -> 898b13a8313d2aec0235f64ed7a584b54cdd9b1f2ba05e5db1c35446b99fe4ea
Branche 2 -> 8241981d28e05664e291fbe5efb0b230ade095350f2639280cb722da091516f4

Hell -> 2e5b7961ede9dfdb4c69811a11b724c407530e50e2d4ee66edc1a8ba05990530
o, W -> b060fc7acde1f9081ab6960cac53e3c6cba13bac171aa1d56192f91aa0774e3c
orld -> af7e10710312284c829aa8a3f05f45b1ff11093754d9bb8b71479a391d734b0c
 !-> a038c6a06dc31ebb67f8527c1aa3934147e9b364ea4e0bf5d41663427d7ff7af

On fait la même chose pour le second texte :

Racine -> 7e7af2183768a714d80a6e30902ffe2717d45fabc5e16986ff46c4b5918ab601

Branche 1 -> 898b13a8313d2aec0235f64ed7a584b54cdd9b1f2ba05e5db1c35446b99fe4ea
Branche 2 -> bf30dd5dca92e70108a4d6bc557cf4cc1a22641bd2c2120e6f1180685ee212bd

Hell -> 2e5b7961ede9dfdb4c69811a11b724c407530e50e2d4ee66edc1a8ba05990530
o, W -> b060fc7acde1f9081ab6960cac53e3c6cba13bac171aa1d56192f91aa0774e3c
arld -> 5bca745103e0fee105a03c0aa8900d92a9baa7f98b2fef39492aa713074b1c50
!-> a038c6a06dc31ebb67f8527c1aa3934147e9b364ea4e0bf5d41663427d7ff7af

En comparant les deux empreintes finales, on peut déduire que les textes sont différents comme on le faisait auparavant. On note au passage que l'empreinte calculée depuis le texte diffère de nos empreintes racines, ce qui est normal : ces dernières sont des empreintes d'empreintes d'empreintes, pas celle correspondant au texte.

En comparant les empreintes de branches on constate que la première est identique, mais pas la seconde. Via les empreintes de feuilles, on voit qu'un bloc sur quatre a changé.

Petites empreintes, gros avantages

Si l'on doit stocker ces deux textes au sein d'un système, on peut donc effectuer une déduplication, en ne stockant pas en double trois des quatre blocs de données. Pour de la gestion de version, on peut également stocker uniquement le bloc qui a été modifié et sa référence. Git a néanmoins adapté ce système à ses besoins.

Le gestionnaire de version développé par Linus Torvalds organise en effet ses données sous la forme d'objets dont des arbres (Tree) qui regroupent des fichiers (Blob). Tous sont identifiés par une signature (SHA-1) et organisés sous la forme d'arbres de hachage. Une organisation à ne pas confondre avec ceux des objets Commit, qui peuvent être reliés entre eux à travers le système de branches et forment plutôt un graphe orienté acyclique (DAG).

L'organisation des objets Tree (à gauche) et Commit (à droite) dans git

L'intérêt de cette méthode, est qu'elle permet une analyse et comparaison sur la base de simples empreintes, pouvant correspondre à de gros blocs de fichiers. Récupérer l'arbre de Merkle d'une image ISO de 5 Go sera très rapide. On pourra alors décider de la télécharger en intégralité ou non selon les blocs de données dont on dispose déjà localement, depuis différents serveurs selon les blocs dont ils disposent et leur débit par exemple.

Dans le cas de Bitcoin et d'autres crypto-monnaies, c'est différent. Les arbres de Merkle sont utilisés pour représenter et valider l'intégrité des blocs de transactions, mais aussi les relier entre eux. Ainsi, le header de chaque bloc contient diverses informations, dont l'empreinte racine du bloc précédent dans la chaîne.

L'identifiant de chaque bloc est une empreinte des informations contenues dans le header. Outre l'intégrité des informations et des transactions, on peut alors vérifier la position du bloc dans la chaîne grâce à son identifiant. 

On pourrait aussi alléger la blockchain stockée (pruning) en ne retenant que certains blocs de transactions et leurs arbres de Merkle. Une solution évoquée dans l'article originel décrivant Bitcoin, mais pas implémentée telle que. Il en va de même pour la Simplified Payment Verification (SPV) qui permet d'effectuer des vérifications en ne stockant pas toute la blockchain mais uniquement les headers des blocs, bien plus légers.

Le pruning, présenté par Satoshi Nakamoto pour économiser de l'espace pour le stockage de la blockchain Bitcoin