Cause -> effet

On commence par deux définitions issues du Larousse. La corrélation, pour commencer, est une « relation existant entre deux notions dont l'une ne peut être pensée sans l'autre, entre deux faits liés par une dépendance nécessaire ».

Quant à la causalité, c’est le « lien qui unit la cause à l'effet », toujours selon dictionnaire en ligne. Dans le film Matrix, le Mérovingien donne un exemple basique de la causalité : « Nous sommes tous victimes de la causalité : chaque fois que je bois trop de vin, il faut que je pisse ! Cause et effet ». Sa femme Perséphone lui donne un autre exemple de causalité peu après.

Passons directement à une locution latine qui résume parfaitement le propos de notre édito du jour : « cum hoc sed non propter hoc signifiant », que l’on peut traduire par « avec ceci, cependant pas à cause de ceci ».

Une manière de dire que corrélation n'implique pas causalité. Il s’agit, comme le rappelle Wikipédia, d’un « raisonnement fallacieux consistant à penser ou prétendre que la corrélation de deux événements impliquerait un lien de causalité entre ceux-ci ». On parle aussi d’effet cigogne.

De belles corrélations, sans aucune causalité

Sur Internet, on trouve des sites qui s’amusent avec ces notions, notamment Spurious correlations et un article du Monde proposé par Bansan dans les commentaires du LIDD. L’idée est la même dans les deux cas : trouver des données qui semblent être des corrélations entre deux événements, mais sans aucune causalité entre les deux.

Quelques exemples. Le coefficient de corrélation entre les dépenses de la défense aux États-Unis et la surface forestière sur le territoire croate est de 96 %. On obtient même 97,3 % sur la consommation d'énergies renouvelables au Danemark face à la proportion de femmes au sein des Parlements des pays de l'Union européenne.

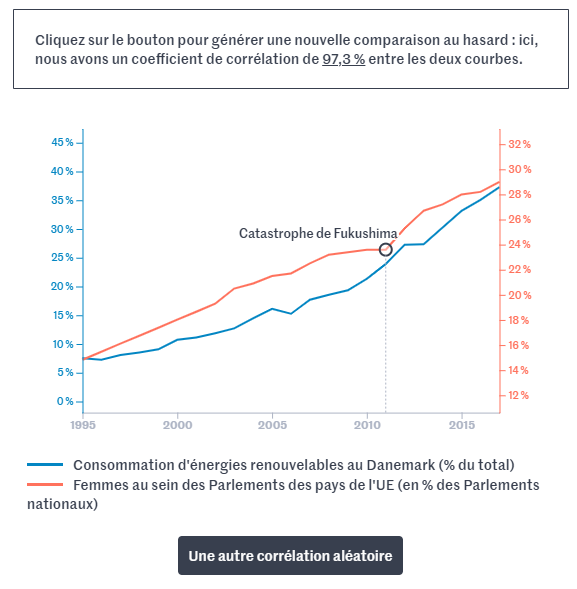
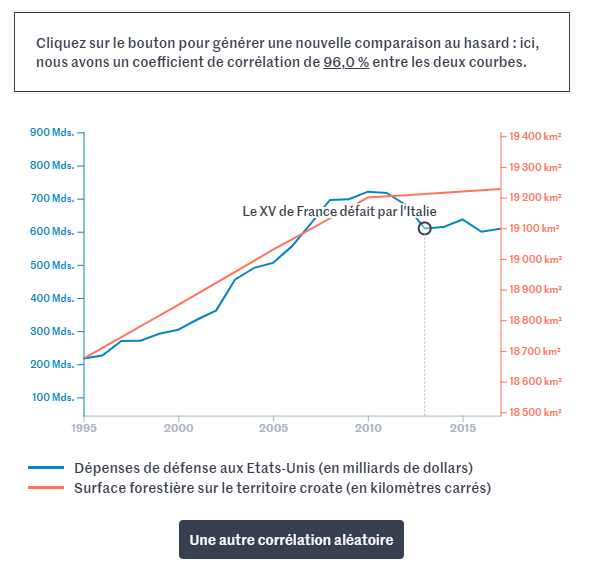
Si les courbes affichent une belle corrélation, il n’y a aucune causalité. Les dépenses de la défense américaine n’ont aucun lien avec la superficie forestière croate, pas plus que la consommation d'énergies renouvelables du Danemark n'implique des conséquences sur la proportion de femmes dans un Parlement.

Et encore, on pourrait dire que le problème de la consommation énergétique et de la place des femmes dans notre société prend de l’importance, ce n’est donc pas surprenant que les deux courbes grimpent au fil des années. Vous l’aurez remarqué, les graphiques ne commencent pas nécessairement à zéro afin de faire coller au mieux les courbes de manière artificielle.

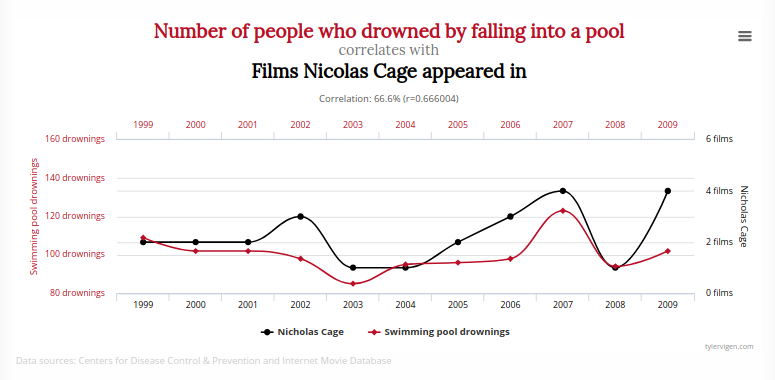
Un exemple qui revient régulièrement dans les médias est la corrélation entre le nombre de films dans lesquels apparait Nicolas Cage et le nombre de morts par noyade dans une piscine. Celle-ci a particulièrement inspiré Flock pour l’illustration de notre édito !

Parfois, la causalité est « cachée »

En dépit de la beauté de ces exemples, il n'y a aucune causalité. Parfois, il existe cependant une causalité « cachée », on parle alors de troisième variable.

Un premier exemple simple pour comprendre de quoi on parle. On peut trouver une corrélation entre les ventes de glaces et les coups de soleil, et la même chose entre les ventes de glace et les noyades. Alors non, manger une glace ne donne pas de coup de soleil et ne fait pas couler les nageurs. Il faut chercher la causalité ailleurs : on mange plus de glace en été, période où l’on prend des coups de soleil et où les baignades sont bien plus fréquentes, avec malheureusement davantage de noyades. La causalité, c’est la météo.

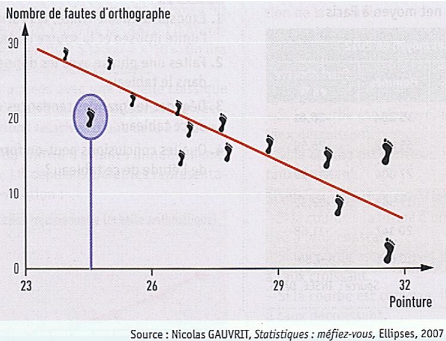
Corrélation entre fautes d'orthographe et taille des pieds

Sur l’espace pédagogique de l’académie de Clermont-Ferrand, on retrouve une fiche méthode sur causalité et corrélation, avec quelques exemples : « Le nombre de fautes d'orthographe et la taille des pieds sont deux variables qui sont corrélées ». On se doute bien que ces variables ne sont pas directement liées : la taille des pieds n’influence pas le nombre de fautes, et vice-versa… et pourtant !

En fait, « c’est l’existence d'une troisième variable "cachée" qui conduit à une corrélation et suggère une relation causale ». Cette troisième variable, c’est l’âge, qui est la cause d'un moindre nombre de fautes et de la taille des pieds. En primaire, les enfants de CM2 font moins de fautes et ont de plus grands pieds que ceux de CP. CQFD.

Même chose avec la corrélation positive « entre la consommation d’alcool et l’espérance de vie : plus on boit d’alcool, et plus l’espérance de vie est élevée ». Ici, on arriverait à une conclusion contraire à la réalité. Si on ajoute une troisième variable cachée, on rétablit les faits. Ainsi, on « observe également que les pays riches sont ceux où l’on boit le plus et ceux où l’on vit le plus longtemps […] c’est donc le revenu par habitant (variable cachée) qui explique à la fois une consommation d’alcool plus élevée (effet de richesse) et une espérance de vie plus longue (meilleur accès à la santé) ».

Et pour ceux qui auraient des doutes, la véritable « relation de cause à effet entre consommation d’alcool et espérance de vie (la première ayant un effet négatif sur la seconde) apparait si l’on compare des pays dont le niveau de richesse est équivalent (PIB/hab proche) ».

D’où l’importance du périmètre et du choix des données… ce qui est aussi valable en statistiques, mais c’est une autre histoire que nous aborderons peut-être un jour. Pour faire simple, on peut faire dire un peu n’importe quoi aux statistiques si on ne sélectionne pas avec soin son échantillon, si on ne donne pas d’intervalle de confiance, etc.

Immigration, délinquance et troisième(s) variable(s)

L’Esprit Critique a également analysé cette troisième variable, avec une approche plus politique sur un sujet qui revient régulièrement sur le devant de la scène : le lien entre immigration et délinquance. « C’est vrai, les étrangers sont surreprésentés dans les chiffres de la délinquance ». La reprise par certains politiques ne s'est évidemment pas fait attendre. Mais pour bien tout comprendre, il faut aussi voir plus loin, avec la notion de troisième variable.

Dans le cas présent, c’est la même chose : « les facteurs de la délinquance sont : le sexe (les hommes sont plus délinquants, immigrés ou pas), la jeunesse (les jeunes sont plus délinquants, immigrés ou pas) ou la situation sociale (la pauvreté est un facteur de délinquance, immigrés ou pas). L’immigration illégale, ce n’est pas des femmes de 60 ans qui gagnent 5 000 balles. Ce sont des jeunes mâles qui n’ont pas un radis ».

Bref, corrélation ne veut pas forcément dire causalité. Il est important de la garder en mémoire, car cela peut conduire à des conclusions hâtives et erronées. Cette réflexion doit se faire à plusieurs niveaux et il est toujours intéressant de se pencher sur ce qu’il y a derrière les chiffres et les affirmations.

Corrélation entre publicités et centres d’intérêt

Dans le cas des smartphones qui nous écoutent, dont Vincent parlait la semaine dernière, il y a bien une relation de causalité entre les publicités affichées et vos centres d’intérêt. Pourtant, les smartphones n’écoutent pas la moindre de vos conversations pour les envoyer sur des serveurs, les retranscrire, etc.

Une troisième variable entre en jeu : vos applications vous surveillent et disposent d’une quantité plus ou moins importante de mouchards, servant de relai au marché publicitaire. Le terme « caché » prend tout son sens dans le marché publicitaire, avec parfois plusieurs centaines de trackers, aussi bien sur des sites que des applications.

• Les smartphones nous espionnent-ils ? Oui, mais pas comme vous le pensez